Electron. J. Differential Equations, Vol. 2020 (2020), No. 69, pp. 1-19
Holder continuity for vector-valued minimizers of quadratic functionals
Josef Danecek, Eugen Viszus
Abstract:
In this article we give a sufficient condition
for interior everywhere Holder continuity of weak minimizers
of a class of quadratic functionals
with coefficients
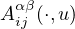 belonging
to the VMO-class, uniformly with respect to
belonging
to the VMO-class, uniformly with respect to
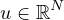 , and
continuous with respect to u.
The condition is global. It is typical for the
functionals belonging to the class that the continuity moduli of their
coefficients become slowly growing sufficiently far from zero. Some
features of the main result are illustrated by examples.
, and
continuous with respect to u.
The condition is global. It is typical for the
functionals belonging to the class that the continuity moduli of their
coefficients become slowly growing sufficiently far from zero. Some
features of the main result are illustrated by examples.
Submitted April 4, 2019. Published July 2, 2020.
Math Subject Classifications: 35J60.
Key Words: Quadratic functionals; minimizers; regularity; Morrey spaces.
DOI: 10.58997/ejde.2020.69
Show me the PDF file (393 KB),
TEX file for this article.
 |
Josef Danecek
VSB - Technical University of Ostrava, FEECS
Department of Applied Mathematics
17. listopadu 15/2172, 70833 Ostrava-Poruba, Czech Republic
email: danecek.j@seznam.cz
|
|---|
 |
Eugen Viszus
Department of Mathematical Analysis and Numerical Mathematics
Faculty of Mathematics, Physics and Informatics
Comenius University, Mlynska dolina
84248 Bratislava, Slovak Republic
email: eugen.viszus@fmph.uniba.sk
|
|---|
Return to the EJDE web page
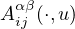 belonging
to the VMO-class, uniformly with respect to
belonging
to the VMO-class, uniformly with respect to
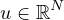 , and
continuous with respect to u.
The condition is global. It is typical for the
functionals belonging to the class that the continuity moduli of their
coefficients become slowly growing sufficiently far from zero. Some
features of the main result are illustrated by examples.
, and
continuous with respect to u.
The condition is global. It is typical for the
functionals belonging to the class that the continuity moduli of their
coefficients become slowly growing sufficiently far from zero. Some
features of the main result are illustrated by examples.

