Electron. J. Differential Equations, Vol. 2020 (2020), No. 74, pp. 1-14
Stability of anisotropic parabolic equations without boundary conditions
Huashui Zhan, Zhaosheng Feng
Abstract:
In this article, we consider the equation
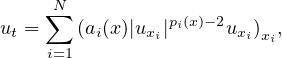
with
 and
and
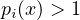 .
Where
.
Where
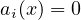 if
if
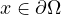 , and
, and
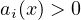 if
if
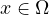 , without
any boundary conditions. We propose an analytical method for studying
the stability of weak solutions. We also study the uniqueness of a weak solution,
and establish its stability under certain conditions.
, without
any boundary conditions. We propose an analytical method for studying
the stability of weak solutions. We also study the uniqueness of a weak solution,
and establish its stability under certain conditions.
Submitted December 9, 2019. Published July 15, 2020.
Math Subject Classifications: 35K15, 35B35, 35K55.
Key Words: Parabolic equation; boundary condition; stability; Holder inequality.
DOI: 10.58997/ejde.2020.74
Show me the PDF file (361 KB),
TEX file for this article.
 |
Huashui Zhan
School of Applied Mathematics
Xiamen University of Technology
Xiamen, Fujian 361024, China
email: 2012111007@xmut.edu.cn
|
|---|
 |
Zhaosheng Feng
School of Mathematical and Statistical Sciences
University of Texas Rio Grande Valley
Edinburg, TX 78539, USA
email: zhaosheng.feng@utrgv.edu
|
|---|
Return to the EJDE web page
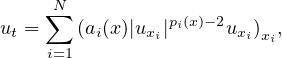
 and
and
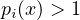 .
Where
.
Where
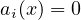 if
if
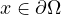 , and
, and
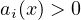 if
if
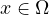 , without
any boundary conditions. We propose an analytical method for studying
the stability of weak solutions. We also study the uniqueness of a weak solution,
and establish its stability under certain conditions.
, without
any boundary conditions. We propose an analytical method for studying
the stability of weak solutions. We also study the uniqueness of a weak solution,
and establish its stability under certain conditions.

