Electron. J. Differential Equations, Vol. 2020 (2020), No. 78, pp. 1-19.
Existence and concentration of positive ground states for Schrodinger-Poisson
equations with competing potential functions
Wenbo Wang, Quanqing Li
Abstract:
This article concerns the Schrodinger-Poisson equation
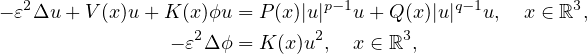
where
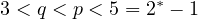 . We prove that for all
. We prove that for all
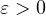 , the equation
has a ground state solution. The methods used here are based on the
Nehari manifold and the concentration-compactness principle.
Furthermore, for
, the equation
has a ground state solution. The methods used here are based on the
Nehari manifold and the concentration-compactness principle.
Furthermore, for
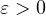 small, these ground states concentrate at
a global minimum point of the least energy function.
small, these ground states concentrate at
a global minimum point of the least energy function.
Submitted January 11, 2019. Published July 22, 2020.
Math Subject Classifications: 35J15, 35J20, 35J50.
Key Words: Schrodinger-Poisson equation; Nehari manifold; ground states;
concentration-compactness; concentration.
DOI: 10.58997/ejde.2020.78
Show me the PDF file (393 KB),
TEX file for this article.
 |
Wenbo Wang
School of Mathematics and Statistics
Yunnan University
Kunming, 650500, Yunnan, China
email: wenbowangmath@163.com
|
|---|
 |
Quanqing Li
Department of Mathematics
Honghe University
Mengzi, 661100, Yunnan, China
email: shili06171987@126.com
|
|---|
Return to the EJDE web page
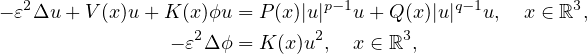
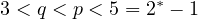 . We prove that for all
. We prove that for all
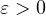 , the equation
has a ground state solution. The methods used here are based on the
Nehari manifold and the concentration-compactness principle.
Furthermore, for
, the equation
has a ground state solution. The methods used here are based on the
Nehari manifold and the concentration-compactness principle.
Furthermore, for
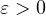 small, these ground states concentrate at
a global minimum point of the least energy function.
small, these ground states concentrate at
a global minimum point of the least energy function.

