Jing Zhang, Chao Ji
Abstract:
This article concerns the quasilinear Schrodinger equation
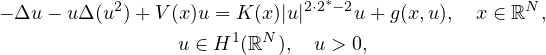
where V and K are positive, continuous and periodic functions,
g(x,u) is periodic in x and has subcritical growth.
We use the generalized Nehari manifold approach developed by Szulkin and Weth
to study the ground state solution, i.e. the nontrivial solution with least
possible energy.
Submitted March 11, 2020. Published July 29, 2020.
Math Subject Classifications: 35A15, 35B33, 35B38.
Key Words: Quasilinear Schrodinger equation; Nehari manifold; ground state.
DOI: 10.58997/ejde.2020.82
Show me the PDF file (348 KB), TEX file for this article.
| Jing Zhang Mathematics Sciences College Inner Mongolia Normal University Hohhot, 010022, China email: jinshizhangjing@163.com | |
 |
Chao Ji Department of Mathematics East China University of Science and Technology Shanghai 200237, China email: jichao@ecust.edu.cn |
Return to the EJDE web page