Electron. J. Differential Equations, Vol. 2020 (2020), No. 85, pp. 1-15.
Stability of initial-boundary value problem for quasilinear viscoelastic equations
Kun-Peng Jin, Jin Liang, Ti-Jun Xiao
Abstract:
We investigate the stability of the initial-boundary value problem for the
quasilinear viscoelastic equation
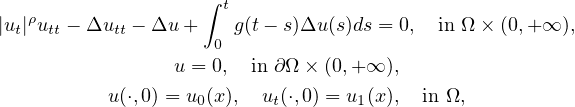
where
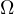 is a bounded domain of
is a bounded domain of
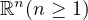 with smooth boundary
with smooth boundary
 ,
,
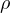 is a positive real number, and g(t) is the relaxation function.
We present a general polynomial decay result under some weak conditions on g, which
generalizes and improves the existing related results.
Moreover, under the condition
is a positive real number, and g(t) is the relaxation function.
We present a general polynomial decay result under some weak conditions on g, which
generalizes and improves the existing related results.
Moreover, under the condition
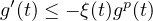 ,
we obtain
uniform exponential and polynomial decay rates for
,
we obtain
uniform exponential and polynomial decay rates for
 ,
while in the
previous literature only the case
,
while in the
previous literature only the case
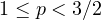 was studied.
Finally, under a general condition
was studied.
Finally, under a general condition
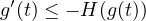 ,
we establish a fine decay
estimate, which is stronger than the previous results.
,
we establish a fine decay
estimate, which is stronger than the previous results.
Submitted November 11, 2019. Published July 30, 2020.
Math Subject Classifications: 35Q74, 35B35, 74H55, 74H40, 93D15.
Key Words: Quasilinear viscoelastic equation; polynomial and exponential decay;
relaxation function; uniform decay.
DOI: 10.58997/ejde.2020.85
Show me the PDF file (357 KB),
TEX file for this article.
Kun-Peng Jin
School of Science
Chongqing University of Posts and Telecommunications
Chongqing 400065, China
email: kjin11@fudan.edu.cn
|
Jin Liang
School of Mathematical Sciences
Shanghai Jiao Tong University
Shanghai 200240, China
email: jinliang@sjtu.edu.cn
|
Ti-Jun Xiao
Shanghai Key Laboratory for Contemporary Applied Mathematics
School of Mathematical Sciences
Fudan University
Shanghai 200433, China
email: tjxiao@fudan.edu.cn
|
Return to the EJDE web page
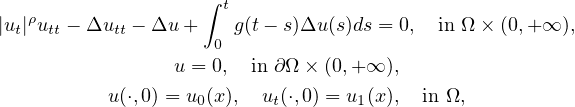
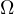 is a bounded domain of
is a bounded domain of
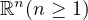 with smooth boundary
with smooth boundary
 ,
,
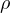 is a positive real number, and g(t) is the relaxation function.
We present a general polynomial decay result under some weak conditions on g, which
generalizes and improves the existing related results.
Moreover, under the condition
is a positive real number, and g(t) is the relaxation function.
We present a general polynomial decay result under some weak conditions on g, which
generalizes and improves the existing related results.
Moreover, under the condition
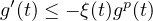 ,
we obtain
uniform exponential and polynomial decay rates for
,
we obtain
uniform exponential and polynomial decay rates for
 ,
while in the
previous literature only the case
,
while in the
previous literature only the case
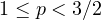 was studied.
Finally, under a general condition
was studied.
Finally, under a general condition
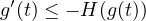 ,
we establish a fine decay
estimate, which is stronger than the previous results.
,
we establish a fine decay
estimate, which is stronger than the previous results.