Electron. J. Differential Equations, Vol. 2020 (2020), No. 89, pp. 1-19.
Fractional-power approach for the study of elliptic second-order
boundary-value problems with variable-operator coefficients
in an unbounded domain
Fatiha Boutaous
Abstract:
In this article, we give new results on the study of elliptic complete abstract
second order differential equations with variable operator coefficients
under Dirichlet boundary conditions, and set in
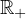 .
In the framework of Holderian spaces and under some compatibility
conditions, we prove the main results on the existence,
uniqueness and maximal regularity of the classical solution of this kind of problems
which have not been studied in variable coefficients case.
We use semigroups theory, fractional powers of linear operators,
Dunford's functional calculus and interpolation theory.
In this work, we consider some differentiability assumptions on the resolvents
of square roots of linear operators.
.
In the framework of Holderian spaces and under some compatibility
conditions, we prove the main results on the existence,
uniqueness and maximal regularity of the classical solution of this kind of problems
which have not been studied in variable coefficients case.
We use semigroups theory, fractional powers of linear operators,
Dunford's functional calculus and interpolation theory.
In this work, we consider some differentiability assumptions on the resolvents
of square roots of linear operators.
Submitted January 12, 2018. Published September 1, 2020.
Math Subject Classifications: 34G10, 34K10, 34K30, 35J25, 44A45, 47D06
Key Words: Fractional powers of linear operators; analytic semigroups;
classical solution; Dunford's functional calculus.
DOI: 10.58997/ejde.2020.89
Show me the PDF file (348 KB),
TEX file for this article.
 |
Fatiha Boutaous
Department of Mathematics
Faculty of Sciences
Saad Dahlab University, 09000, Blida, Algeria
email: boutaous.fatiha2009@hotmail.com
|
|---|
Return to the EJDE web page
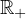 .
In the framework of Holderian spaces and under some compatibility
conditions, we prove the main results on the existence,
uniqueness and maximal regularity of the classical solution of this kind of problems
which have not been studied in variable coefficients case.
We use semigroups theory, fractional powers of linear operators,
Dunford's functional calculus and interpolation theory.
In this work, we consider some differentiability assumptions on the resolvents
of square roots of linear operators.
.
In the framework of Holderian spaces and under some compatibility
conditions, we prove the main results on the existence,
uniqueness and maximal regularity of the classical solution of this kind of problems
which have not been studied in variable coefficients case.
We use semigroups theory, fractional powers of linear operators,
Dunford's functional calculus and interpolation theory.
In this work, we consider some differentiability assumptions on the resolvents
of square roots of linear operators.
