Electron. J. Differential Equations, Vol. 2020 (2020), No. 98, pp. 1-29.
Nehari manifold approach for fractional p(.)-Laplacian system involving
concave-convex nonlinearities
Reshmi Biswas, Sweta Tiwari
Abstract:
In this article, using Nehari manifold method we study the multiplicity of solutions
of the nonlocal elliptic system involving variable exponents
and concave-convex nonlinearities,
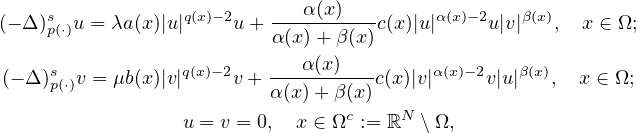
where
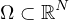 ,
,
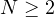 is a smooth bounded domain,
is a smooth bounded domain,
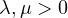 are parameters, and
are parameters, and
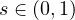 .
We show that there exists
.
We show that there exists
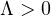 such that for all
such that for all
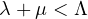 ,
this system admits at least two non-trivial and non-negative solutions under some
assumptions on
,
this system admits at least two non-trivial and non-negative solutions under some
assumptions on
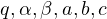 .
.
Submitted November 2, 2019. Published September 23, 2020.
Math Subject Classifications: 35J48, 35J50, 35R11.
Key Words: Nonlocal problem with variable exponents; elliptic system;
Nehari manifold; fibering map; concave-convex nonlinearities.
DOI: 10.58997/ejde.2020.98
Show me the PDF file (445 KB),
TEX file for this article.
 |
Reshmi Biswas
Department of Mathematics
IIT Guwahati, Assam 781039, India
email: b.reshmi@iitg.ac.in
|
|---|
 |
Sweta Tiwari
Department of Mathematics
IIT Guwahati, Assam 781039, India
email: swetatiwari@iitg.ac.in
|
|---|
Return to the EJDE web page
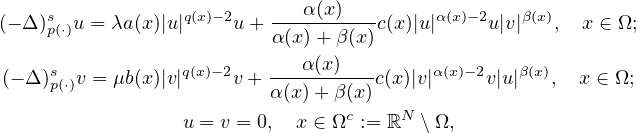
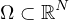 ,
,
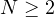 is a smooth bounded domain,
is a smooth bounded domain,
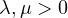 are parameters, and
are parameters, and
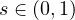 .
We show that there exists
.
We show that there exists
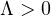 such that for all
such that for all
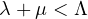 ,
this system admits at least two non-trivial and non-negative solutions under some
assumptions on
,
this system admits at least two non-trivial and non-negative solutions under some
assumptions on
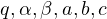 .
.

