Electron. J. Differential Equations, Vol. 2021 (2021), No. 03, pp. 1-17.
Existence and nonexistence for singular sublinear problems on exterior domains
Mageed Ali, Joseph A. Iaia
Abstract:
In this article we study the existence of radial solutions of
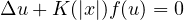 on the exterior of the ball of radius R>0 centered at the origin in
on the exterior of the ball of radius R>0 centered at the origin in
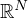 with u=0 on
with u=0 on
 , and
, and
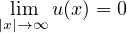 where N>2,
where N>2,
 for u near 0 with 0<q<1, and
for u near 0 with 0<q<1, and
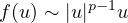 for large |u| with 0<p<1.
Also,
for large |u| with 0<p<1.
Also,
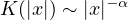 with
with
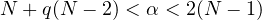 for large |x|.
for large |x|.
Submitted June 11, 2020. Published January 7, 2021.
Math Subject Classifications: 34B40, 35B05.
Key Words: Exterior domains; singular problem; sublinear; radial solution.
DOI: https://doi.org/10.58997/ejde.2021.03
Show me the PDF file (375 KB),
TEX file for this article.
 |
Mageed Ali
Department of Mathematics
University of North Texas, P.O. Box 311430
Denton, TX 76203-5017, USA
email: mageedali@my.unt.edu
|
|---|
 |
Joseph A. Iaia
Department of Mathematics
University of North Texas, P.O. Box 311430
Denton, TX 76203-5017, USA
email: iaia@unt.edu
|
|---|
Return to the EJDE web page
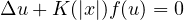 on the exterior of the ball of radius R>0 centered at the origin in
on the exterior of the ball of radius R>0 centered at the origin in
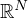 with u=0 on
with u=0 on
 , and
, and
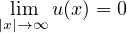 where N>2,
where N>2,
 for u near 0 with 0<q<1, and
for u near 0 with 0<q<1, and
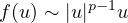 for large |u| with 0<p<1.
Also,
for large |u| with 0<p<1.
Also,
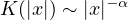 with
with
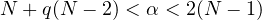 for large |x|.
for large |x|.

