Electron. J. Differential Equations, Vol. 2021 (2021), No. 04, pp. 1-11.
An asymptotic monotonicity formula for minimizers of
elliptic systems of Allen-Cahn type and the Liouville property
Christos Sourdis
Abstract:
We prove an asymptotic monotonicity formula for bounded, globally
minimizing solutions (in the sense of Morse) to a class of semilinear elliptic systems of
the form
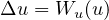 ,
,
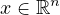 ,
,
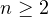 ,
with
,
with
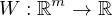 ,
,
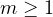 ,
nonnegative and
vanishing at exactly one point (at least in the closure of the
image of the considered solution
,
nonnegative and
vanishing at exactly one point (at least in the closure of the
image of the considered solution
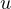 ). As an application, we can
prove a Liouville type theorem under various assumptions.
). As an application, we can
prove a Liouville type theorem under various assumptions.
Submitted January 21, 2019. Published January 20, 2021.
Math Subject Classifications: 35J48, 35J20, 35J61.
Key Words: Entire solutions; monotonicity formula; Allen-Cahn equation;
Liouville theorem; multi-phase transitions.
DOI: https://doi.org/10.58997/ejde.2021.??04
Show me the PDF file (345 KB),
TEX file for this article.
 |
Christos Sourdis
Department of Mathematics
National and Kapodistrian University of Athens
Athens, Greece
email: sourdis@uoc.gr
|
|---|
Return to the EJDE web page
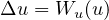 ,
,
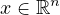 ,
,
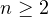 ,
with
,
with
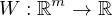 ,
,
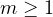 ,
nonnegative and
vanishing at exactly one point (at least in the closure of the
image of the considered solution
,
nonnegative and
vanishing at exactly one point (at least in the closure of the
image of the considered solution
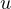 ). As an application, we can
prove a Liouville type theorem under various assumptions.
). As an application, we can
prove a Liouville type theorem under various assumptions.
