We consider a variant of a nonlinear parabolic system, proposed by Gilad, von Hardenberg, Provenzale, Shachak and Meron, in desertification studies, in which there is a strong absorption. The system models the mutual interaction between the biomass, the soil-water content w and the surface-water height which is diffused by means of the degenerate operator
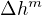with m≥ 2.
The main novelty in this article is that the absorption is given in terms of
an exponent
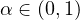, in contrast to the case
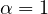considered
in the previous literature. Thanks to this, some new qualitative behavior of
the dynamics of the solutions can be justified.
After proving the existence of non-negative solutions for the system with
Dirichlet and Neumann boundary conditions, we demonstrate the possible
extinction in finite time and the finite speed of propagation for the
surface-water height component h(t,x). Also, we prove, for the associate stationary
problem, that if the precipitation datum
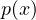grows near the boundary of
the domain
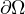as
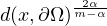then
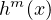grows, at most, as
.
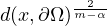This property also implies the infinite waiting time property when the initial datum
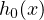grows at fast as
near the
boundary of its support
.
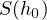