Electron. J. Differential Equations, Vol. 2021 (2021), No. 101, pp. 1-23.
Global well-posedness for Klein-Gordon-Hartree and fractional Hartree equations
on modulation spaces
Divyang G. Bhimani
Abstract:
We study the Cauchy problems for the Klein-Gordon (HNLKG), wave (HNLW),
and Schrodinger (HNLS) equations with cubic convolution (of Hartree type) nonlinearity.
Some global well-posedness and scattering are obtained for the (HNLKG) and (HNLS)
with small Cauchy data in some modulation spaces. Global well-posedness for fractional
Schrodinger (fNLSH) equation with Hartree type nonlinearity is obtained with
Cauchy data in some modulation spaces. Local well-posedness for (HNLW), (fHNLS) and
(HNLKG) with rough data in modulation spaces is shown. As a consequence, we get local
and global well-posedness and scattering in larger than usual
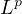 -Sobolev spaces.
-Sobolev spaces.
Submitted April 30, 2021. Published December 21, 2021.
Math Subject Classifications: 35L71, 35Q55, 42B35, 35A01.
Key Words: Klein-Gordon-Hartree equation; fractional Hartree equation;
wave-Hartree equation; well-posedness; modulation spaces; small initial data.
DOI: https://doi.org/10.58997/ejde.2021.101
Show me the PDF file (422 KB),
TEX file for this article.
 |
Divyang G. Bhimani
Department of Mathematics
Indian Institute of Science Education and Research
Dr. Homi Bhabha Road, Pune 411008, India
email: divyang.bhimani@iiserpune.ac.in
|
|---|
Return to the EJDE web page
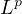 -Sobolev spaces.
-Sobolev spaces.
