Electron. J. Differential Equations, Vol. 2021 (2021), No. 11, pp. 1-17.
Existence of solutions for critical fractional p-Laplacian equations with
indefinite weights
Na Cui, Hong-Rui Sun
Abstract:
This article concerns the critical fractional p-Laplacian equation
with indefinite weights

where
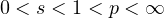 ,
,
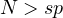 and
and
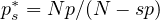 , the weight functions g
may be indefinite, and h changes sign. Specifically, based on the results of
asymptotic estimates for an extremal in the fractional Sobolev inequality and
the discrete spectrum of fractional p-Laplacian operator, we establish
an existence criterion for a nontrivial solution to this problem.
, the weight functions g
may be indefinite, and h changes sign. Specifically, based on the results of
asymptotic estimates for an extremal in the fractional Sobolev inequality and
the discrete spectrum of fractional p-Laplacian operator, we establish
an existence criterion for a nontrivial solution to this problem.
Submitted April 1, 2020. Published March 5, 2021.
Math Subject Classifications: 35R11, 35J92, 35B33.
Key Words: Fractional p-Laplacian; critical exponent; indefinite weight.
DOI: https://doi.org/10.58997/ejde.2021.11
Show me the PDF file (376 KB),
TEX file for this article.
 |
Na Cui
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: cuin17@lzu.edu.cn
|
|---|
 |
Hong-Rui Sun
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: hrsun@lzu.edu.cn
|
|---|
Return to the EJDE web page

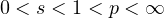 ,
,
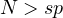 and
and
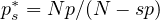 , the weight functions g
may be indefinite, and h changes sign. Specifically, based on the results of
asymptotic estimates for an extremal in the fractional Sobolev inequality and
the discrete spectrum of fractional p-Laplacian operator, we establish
an existence criterion for a nontrivial solution to this problem.
, the weight functions g
may be indefinite, and h changes sign. Specifically, based on the results of
asymptotic estimates for an extremal in the fractional Sobolev inequality and
the discrete spectrum of fractional p-Laplacian operator, we establish
an existence criterion for a nontrivial solution to this problem.

