Electron. J. Differential Equations, Vol. 2021 (2021), No. 15, pp. 1-13.
Asymptotic behavior for a quasi-autonomous gradient system of expansive
type governed by a quasiconvex function
Behzad Djafari Rouhani, Mohsen Rahimi Piranfar
Abstract:
We consider the quasi-autonomous first-order gradient system

where
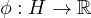 is a differentiable quasiconvex function such that
is a differentiable quasiconvex function such that
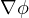 is Lipschitz continuous. We study the asymptotic behavior of solutions to this system in
continuous and discrete time. We show that each solution either approaches
infinity in norm or converges weakly to a critical point of φ.
This further concludes that the existence of bounded solutions and implies that φ has a
nonempty set of critical points. Some strong convergence results, as well as numerical examples,
are also given in both continuous and discrete cases.
is Lipschitz continuous. We study the asymptotic behavior of solutions to this system in
continuous and discrete time. We show that each solution either approaches
infinity in norm or converges weakly to a critical point of φ.
This further concludes that the existence of bounded solutions and implies that φ has a
nonempty set of critical points. Some strong convergence results, as well as numerical examples,
are also given in both continuous and discrete cases.
Submitted January 25, 2021. Published March 18, 2021.
Math Subject Classifications: 34G20, 47J35, 39A30, 37N40.
Key Words: First-order evolution equation; expansive type gradient system;
asymptotic behavior; quasiconvex function; minimization.
DOI: https://doi.org/10.58997/ejde.2021.15
Show me the PDF file (325 KB),
TEX file for this article.
 |
Behzad Djafari Rouhani
Department of Mathematical Sciences
University of Texas at El Paso
500 W. University Ave., El Paso, TX 79968, USA
email: behzad@utep.edu
|
|---|
 |
Mohsen Rahimi Piranfar
Isfahan Mathematics House
Isfahan, Iran
email: m.piranfar@gmail.com
|
|---|
Return to the EJDE web page

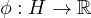 is a differentiable quasiconvex function such that
is a differentiable quasiconvex function such that
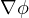 is Lipschitz continuous. We study the asymptotic behavior of solutions to this system in
continuous and discrete time. We show that each solution either approaches
infinity in norm or converges weakly to a critical point of φ.
This further concludes that the existence of bounded solutions and implies that φ has a
nonempty set of critical points. Some strong convergence results, as well as numerical examples,
are also given in both continuous and discrete cases.
is Lipschitz continuous. We study the asymptotic behavior of solutions to this system in
continuous and discrete time. We show that each solution either approaches
infinity in norm or converges weakly to a critical point of φ.
This further concludes that the existence of bounded solutions and implies that φ has a
nonempty set of critical points. Some strong convergence results, as well as numerical examples,
are also given in both continuous and discrete cases.

