Electron. J. Differential Equations, Vol. 2021 (2021), No. 21, pp. 1-14.
Solutions of Kirchhoff plate equations with internal damping and logarithmic nonlinearity
Ducival Pereira, Sebastiao Cordeiro, Carlos Raposo, Celsa Maranhao
Abstract:
In this article we study the existence of weak solutions
for the nonlinear initial boundary value problem of the Kirchhoff equation
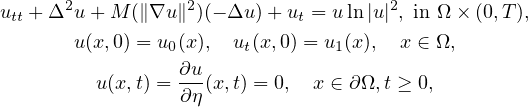
where Ω is a bounded domain in R2 with smooth boundary
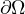 ,
T>0 is a fixed but arbitrary real number,
M(s) is a continuous function on
,
T>0 is a fixed but arbitrary real number,
M(s) is a continuous function on
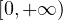 and η is the unit outward
normal on
and η is the unit outward
normal on 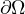 .
Our results are obtained using the Galerkin method, compactness approach,
potential well corresponding to the logarithmic nonlinearity, and the energy estimates
due to Nakao.
.
Our results are obtained using the Galerkin method, compactness approach,
potential well corresponding to the logarithmic nonlinearity, and the energy estimates
due to Nakao.
Submitted May 19, 2020. Published March 29, 2021.
Math Subject Classifications: 35L15, 35L70, 35B40, 35A01
Key Words: Extensible beam; existence of solutions; asymptotic behavior; logarithmic source term.
DOI: https://doi.org/10.58997/ejde.2021.21
Show me the PDF file (352 KB),
TEX file for this article.
 |
Ducival Pereira
Department of Mathematics
State University of Pará
Belém, PA 66113-200, Brazil
email: ducival@uepa.br
|
|---|
 |
Sebastião Cordeiro
Faculty of Exact Sciences and Technology
Federal University of Pará
Abaetetuba, PA 68440-000, Brazil
email: sebastiao@ufpa.br
|
|---|
 |
Carlos Raposo
Department of Mathematics
Federal University of São João del-Rei
São João del-Rei, MG 36307-352, Brazil
email: raposo@ufsj.edu.br
|
|---|
 |
Celsa Maranhão
Department of Mathematics
Federal University of Pará
Belém, PA 66075-110, Brazil
email: celsa@ufpa.br
|
|---|
Return to the EJDE web page
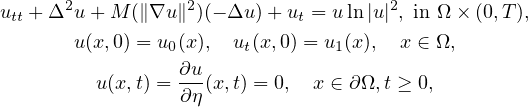
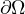 ,
T>0 is a fixed but arbitrary real number,
M(s) is a continuous function on
,
T>0 is a fixed but arbitrary real number,
M(s) is a continuous function on
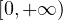 and η is the unit outward
normal on
and η is the unit outward
normal on 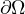 .
Our results are obtained using the Galerkin method, compactness approach,
potential well corresponding to the logarithmic nonlinearity, and the energy estimates
due to Nakao.
.
Our results are obtained using the Galerkin method, compactness approach,
potential well corresponding to the logarithmic nonlinearity, and the energy estimates
due to Nakao.



