Electron. J. Differential Equations, Vol. 2021 (2021), No. 24, pp. 1-13.
Small data blow-up of solutions to nonlinear Schrodinger equations without
gauge invariance in L^2
Yuanyuan Ren, Yongsheng Li
Abstract:
In this article we study the Cauchy problem of the nonlinear Schrodinger equations
without gauge invariance

where 1<p1, p2<1+4/n and
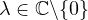 .
We first prove the existence of a local solution with initial data in
L2(Rn).
Then under a suitable condition on the initial data, we show that the L2-norm of the
solution must blow up in finite time although the initial data are arbitrarily small.
As a by-product, we also obtain an upper bound of the maximal existence time of the solution.
.
We first prove the existence of a local solution with initial data in
L2(Rn).
Then under a suitable condition on the initial data, we show that the L2-norm of the
solution must blow up in finite time although the initial data are arbitrarily small.
As a by-product, we also obtain an upper bound of the maximal existence time of the solution.
Submitted February 15, 2018. Published March 31, 2021.
Math Subject Classifications: 35Q55, 35B44.
Key Words: Nonlinear Schrodinger equations; weak solution; blow up of solutions.
DOI: https://doi.org/10.58997/ejde.2021.24
Show me the PDF file (357 KB),
TEX file for this article.
 |
Yuanyuan Ren
School of Computer Science and Technology
Dongguan University of Technology
Dongguan, Guangdong 523808, China
email: renyuanzhpp@163.com
|
|---|
| |
Yongsheng Li
School of Mathematics
South China University of Technology
Guangzhou, Guangdong 510640, China
email: yshli@scut.edu.cn
|
|---|
Return to the EJDE web page

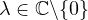 .
We first prove the existence of a local solution with initial data in
L2(Rn).
Then under a suitable condition on the initial data, we show that the L2-norm of the
solution must blow up in finite time although the initial data are arbitrarily small.
As a by-product, we also obtain an upper bound of the maximal existence time of the solution.
.
We first prove the existence of a local solution with initial data in
L2(Rn).
Then under a suitable condition on the initial data, we show that the L2-norm of the
solution must blow up in finite time although the initial data are arbitrarily small.
As a by-product, we also obtain an upper bound of the maximal existence time of the solution.
