Electron. J. Differential Equations, Vol. 2021 (2021), No. 31, pp. 1-19.
Existence and multiplicity for radially symmetric solutions to Hamilton-Jacobi-Bellman equations
Xiaoyan Li, Bian-Xia Yang
Abstract:
This article concerns the existence and multiplicity of radially symmetric
nodal solutions to the nonlinear equation
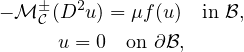
where
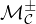 are general Hamilton-Jacobi-Bellman operators,
μ is a real parameter and
are general Hamilton-Jacobi-Bellman operators,
μ is a real parameter and
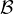 is the unit ball.
By using bifurcation theory, we determine the range of parameter μ in which the
above problem has one or multiple nodal solutions according to the behavior of f
at 0 and infinity, and whether f satisfies the signum condition f(s)s>0 for
is the unit ball.
By using bifurcation theory, we determine the range of parameter μ in which the
above problem has one or multiple nodal solutions according to the behavior of f
at 0 and infinity, and whether f satisfies the signum condition f(s)s>0 for
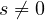 or not.
or not.
Submitted November 29, 2020. Published April 24, 2021.
Math Subject Classifications: 35B32, 35B40, 35B45, 35J60, 34C23.
Key Words: Radially symmetric solution; extremal operators; bifurcation; nodal solution.
DOI: https://doi.org/10.58997/ejde.2021.31
Show me the PDF file (444 KB),
TEX file for this article.
 |
Xiaoyan Li
Department of Mathematics and Statistics
Northwest Normal University
Lanzhou, Gansu 730000, China
email: 17242502@qq.com
|
|---|
 |
Bian-Xia Yang
College of Science
Northwest A&F University
Yangling, Shaanxi 712100, China
email: yanglina7765309@163.com
|
|---|
Return to the EJDE web page
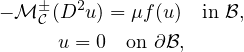
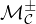 are general Hamilton-Jacobi-Bellman operators,
μ is a real parameter and
are general Hamilton-Jacobi-Bellman operators,
μ is a real parameter and
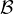 is the unit ball.
By using bifurcation theory, we determine the range of parameter μ in which the
above problem has one or multiple nodal solutions according to the behavior of f
at 0 and infinity, and whether f satisfies the signum condition f(s)s>0 for
is the unit ball.
By using bifurcation theory, we determine the range of parameter μ in which the
above problem has one or multiple nodal solutions according to the behavior of f
at 0 and infinity, and whether f satisfies the signum condition f(s)s>0 for
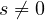 or not.
or not.

