Electron. J. Differential Equations, Vol. 2021 (2021), No. 32, pp. 1-12.
Improved oscillation criteria for first-order delay differential equations
with variable delay
Julio G. Dix
Abstract:
This article concerns the oscillation of solutions to the delay differential equation
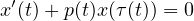 .
Conditions for oscillation have been stated as lower bounds for the limit superior and
limit inferior of
.
Conditions for oscillation have been stated as lower bounds for the limit superior and
limit inferior of
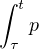 .
In this article we match the bound for the best case in [7],
without using one of their hypotheses.
Then assuming that hypothesis, we obtain a bound lower than the one in [12].
Then we apply our results to an equation with several delays.
We employ iterated estimates of the solution.
.
In this article we match the bound for the best case in [7],
without using one of their hypotheses.
Then assuming that hypothesis, we obtain a bound lower than the one in [12].
Then we apply our results to an equation with several delays.
We employ iterated estimates of the solution.
Submitted January 29, 2021. Published April 24, 2021.
Math Subject Classifications: 34K11, 34C10.
Key Words: Oscillation of solutions; first-order delay differential equation;
eventually positive solution.
DOI: https://doi.org/10.58997/ejde.2021.32
An addendum was posted on October 13, 2022. It indicates that the proof
of Lemma 2.2 is incorrect. See the last page of this article.
Show me the PDF file (326 KB),
TEX file for this article.
 |
Julio G. Dix
Department of Mathematics
Texas State University
601 University Drive
San Marcos, TX 78666, USA
email: jd01@txstate.edu
|
|---|
Return to the EJDE web page
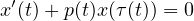 .
Conditions for oscillation have been stated as lower bounds for the limit superior and
limit inferior of
.
Conditions for oscillation have been stated as lower bounds for the limit superior and
limit inferior of
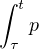 .
In this article we match the bound for the best case in [7],
without using one of their hypotheses.
Then assuming that hypothesis, we obtain a bound lower than the one in [12].
Then we apply our results to an equation with several delays.
We employ iterated estimates of the solution.
.
In this article we match the bound for the best case in [7],
without using one of their hypotheses.
Then assuming that hypothesis, we obtain a bound lower than the one in [12].
Then we apply our results to an equation with several delays.
We employ iterated estimates of the solution.
