We consider a general 3-dimensional Lotka-Volterra system with a rational first integral of degree two of the form H=xI yjk. The restriction of this Lotka-Volterra system to each surface H(x,y,z)=h varying h in R provide Kolmogorov systems. With the additional assumption that they have a Darboux invariant of the form x
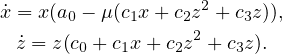
We classify the phase portraits in the Poincare disc of all these Kolmogorov systems which depend on six parameters.
Submitted June 1, 2020. Published May 3, 2021.
Math Subject Classifications: 34C05.
Key Words: Kolmogorov system; Lotka-Volterra system; phase portrait; Poincare disc
DOI: https://doi.org/10.58997/ejde.2021.35
Show me the PDF file (862 KB), TEX file for this article.
 |
Érika Diz-Pita Departamento de Estatística Análise Matemática e Optimización Universidade de Santiago de Compostela 15782 Santiago de Compostela, Spain email: erikadiz.pita@usc.es |
|---|---|
 |
Jaume Llibre Departament de Matemàtiques Universitat Autònoma de Barcelona 08193 Bellaterra, Barcelona, Spain email: jllibre@mat.uab.cat |
 |
M. Victoria Otero-Espinar Departamento de Estatística Análise Matemática e Optimización Universidade de Santiago de Compostela 15782 Santiago de Compostela, Spain email: mvictoria.otero@usc.es |
Return to the EJDE web page