Electron. J. Differential Equations, Vol. 2021 (2021), No. 39, pp. 1-18.
Blow-up criteria and instability of standing waves for the inhomogeneous
fractional Schrodinger equation
Binhua Feng, Zhiqian He, Jiayin Liu
Abstract:
In this article, we study the blow-up and instability of standing waves for the
inhomogeneous fractional Schrodinger equation
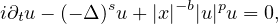
where
 ,
,
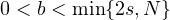 and
and
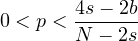 .
In the L2-critical and L2-supercritical cases, i.e.,
.
In the L2-critical and L2-supercritical cases, i.e.,
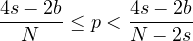 , we establish general blow-up criteria
for non-radial solutions by using localized virial estimates. Based on these
blow-up criteria, we prove the strong instability of standing waves.
, we establish general blow-up criteria
for non-radial solutions by using localized virial estimates. Based on these
blow-up criteria, we prove the strong instability of standing waves.
Submitted November 28, 2020. Published May 7, 2021.
Math Subject Classifications: 35B35, 35B40, 35K57, 35Q92, 92C17.
Key Words: Inhomogeneous fractional Schrodinger equation; blow-up criteria;
strong instability.
DOI: https://doi.org/10.58997/ejde.2021.39
Show me the PDF file (396 KB),
TEX file for this article.
 |
Binhua Feng
Department of Mathematics
Northwest Normal University
Lanzhou,730070, China
email: binhuaf@163.com
|
|---|
| |
Zhiqian He
Department of Basic Teaching and Research
Qinghai University
Xining 810016, China
email: zhiqianhe1987@163.com
|
|---|
 |
Jiayin Liu
School of Mathematics and Information Science
North Minzu University
Yinchuan 750021, China
email: xecd@163.com
|
|---|
Return to the EJDE web page
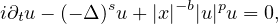
 ,
,
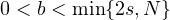 and
and
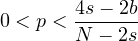 .
In the L2-critical and L2-supercritical cases, i.e.,
.
In the L2-critical and L2-supercritical cases, i.e.,
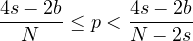 , we establish general blow-up criteria
for non-radial solutions by using localized virial estimates. Based on these
blow-up criteria, we prove the strong instability of standing waves.
, we establish general blow-up criteria
for non-radial solutions by using localized virial estimates. Based on these
blow-up criteria, we prove the strong instability of standing waves.

