Wei-Chuan Wang
Abstract:
In this article, we study the nonlinear equation
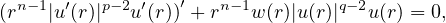
where q>p>1. For positive potentials (w>0), we investigate the existence of
sign-changing solutions with prescribed number of zeros depending on the increasing
initial parameters. For negative potentials, we deduce a finite interval in which
the positive solution will tend to infinity.
The main methods using in this work are the scaling argument, Prufer-type substitutions,
and some integrals involving the p-Laplacian.
Submitted September 8, 2020. Published May 7, 2021.
Math Subject Classifications: 34A12, 34B15, 34A55.
Key Words: Nonlinear p-Laplacian equation; sign-changing solution; blow-up solution.
DOI: https://doi.org/10.58997/ejde.2021.40
Show me the PDF file (387 KB), TEX file for this article.
 |
Wei-Chuan Wang Center for General Education National Quemoy University Kinmen, Taiwan 892, ROC email: wangwc@nqu.edu.tw, wangwc72@gmail.com |
|---|
Return to the EJDE web page