Electron. J. Differential Equations, Vol. 2021 (2021), No. 44, pp. 1-25.
Entire solutions for the heat equation
Vassilis G. Papanicolaou, Eva Kallitsi, George Smyrlis
Abstract:
We consider the solutions of the heat equation
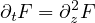
which are entire in z and t (caloric functions).
We examine the relation of the z-order and z-type of an entire caloric function
F(t, z), viewed as function of z, to its t-order and t-type respectively,
if it is viewed as function of t.
Also, regarding the zeros zk(t) of an entire caloric function F(t, z), viewed as
function of z, we show that the points (t, z) at which

form a discrete set in
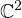 and, then, we derive the t-evolution equations
of zk(t). These are differential equations that hold for all but countably many
ts in
and, then, we derive the t-evolution equations
of zk(t). These are differential equations that hold for all but countably many
ts in 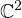 .
.
Submitted October 20, 2020. Published May 25, 2021.
Math Subject Classifications: 35KO5, 32W30.
Key Words: Entire solution; heat equation; entire caloric functions; order;
dynamics of the zeros.
DOI: https://doi.org/10.58997/ejde.2021.44
Show me the PDF file (422 KB),
TEX file for this article.
 |
Vassilis G. Papanicolaou
National Technical University of Athens
Zografou Campus, 157 80, Athens, Greece
email: papanico@math.ntua.gr
|
|---|
 |
Eva Kallitsi
National Technical University of Athens
Zografou Campus, 157 80, Athens, Greece
email: evpapa@hotmail.com
|
|---|
 |
George Smyrlis
National Technical University of Athens
Zografou Campus, 157 80, Athens, Greece
email: gsmyrlis@math.ntua.gr
|
|---|
Return to the EJDE web page
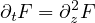

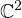 and, then, we derive the t-evolution equations
of zk(t). These are differential equations that hold for all but countably many
ts in
and, then, we derive the t-evolution equations
of zk(t). These are differential equations that hold for all but countably many
ts in 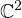 .
.


