Electron. J. Differential Equations, Vol. 2021 (2021), No. 50, pp. 1-23.
Asymptotic formulas for q-regularly varying solutions of half-linear q-difference equations
Katarina S. Djordjevic
Abstract:
This article studies the asymptotic behavior of positive solutions of the q-difference
half-linear equation
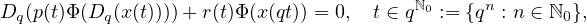
where q>1, Φ(x)=|x|αsgn x,
α >0, p:qN0 → (0,∞),
r: qN0 → R, in the framework of
q-regular variation. In particular, if r is eventually of one sign, p and |r|
are q-regularly varying functions such that tα+1 r(t)/p(t) → 0,
as t → ∞, we obtain asymptotic formulas for the q-regularly varying solutions.
Moreover, when p(t)= 1 and r is an eventually positive or
eventually negative function, we obtain an asymptotic formula of a q-slowly varying solution.
Using generalized regularly varying sequences, we apply these results to the
half-linear difference equation case. At the end, we illustrate the obtained results
with examples.
Submitted February 28, 2021. Published June 8, 2021.
Math Subject Classifications: 26A12, 39A13, 39A22.
Key Words: q-difference equation; non-oscillatory solution; asymptotic behavior;
regular variation; q-regular variation; half-linear equation.
DOI: https://doi.org/10.58997/ejde.2021.50
Show me the PDF file (418 KB),
TEX file for this article.
 |
Katarina S. Djordjevic
Department of Mathematics
University of Nis, Faculty of Science and Mathematics
Visegradska 33, 18000 Nis, Serbia
email: katarina.kostadinov@pmf.edu.rs
|
|---|
Return to the EJDE web page