Electron. J. Differential Equations, Vol. 2021 (2021), No. 52, pp. 1-24.
Existence of positive solutions for Brezis-Nirenberg type problems
involving an inverse operator
Pablo Alvarez-Caudevilla, Eduardo Colorado, Alejandro Ortega
Abstract:
This article concerns the existence of positive solutions for the
second order equation involving a nonlocal term
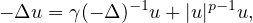
under Dirichlet boundary conditions. We prove the existence of
positive solutions depending on the positive real parameter
γ>0, and up to the critical value of the exponent p, i.e. when
1<p<q; 2*-1, where 2*=(2N)/(N-2) is the critical Sobolev
exponent. For p=2*-1, this leads us to a Brezis-Nirenberg type
problem, cf. [5], but, in our particular case, the linear term
is a nonlocal term. The effect that this nonlocal term has on the
equation changes the dimensions for which the classical technique
based on the minimizers of the Sobolev constant, that ensures the
existence of positive solution, going from dimensions N≥4 in
the classical Brezis-Nirenberg problem, to dimensions N≥7 for
this nonlocal problem.
Submitted November 3, 2020. Published June 14, 2021.
Math Subject Classifications: 35G20, 35A15, 35J50, 35B38, 35J91.
Key Words: Critical point; concentration compactness principle;
mountain pass theorem.
DOI: https://doi.org/10.58997/ejde.2021.52
Show me the PDF file (418 KB),
TEX file for this article.
 |
Pablo Álvarez-Caudevilla
Departamento de Matemáticas
Universidad Carlos III de Madrid
Av. Universidad 30, 28911, Leganés, Madrid, Spain
email: pacaudev@math.uc3m.es
|
|---|
 |
Eduardo Colorado
Departamento de Matemáticas
Universidad Carlos III de Madrid
Av. Universidad 30, 28911, Leganés, Madrid, Spain
email: ecolorad@math.uc3m.es
|
|---|
 |
Alejandro Ortega
Departamento de Matemáticas
Universidad Carlos III de Madrid
Av. Universidad 30, 28911, Leganés, Madrid, Spain
email: alortega@math.uc3m.es
|
|---|
Return to the EJDE web page