Electron. J. Differential Equations, Vol. 2021 (2021), No. 62, pp. 1-14.
Smallest eigenvalues for boundary value problems of two term
fractional differential operators depending on fractional boundary conditions
Paul W. Eloe, Jeffrey T. Neugebauer
Abstract:
Let n≥2 be an integer, and let n-1<α≤n. We consider eigenvalue problems
for two point n-1 ,1 boundary value problems

where 0≤ β ≤n-1 and
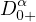 and
and
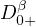 denote standard
Riemann-Liouville differential operators. We prove the existence of smallest positive
eigenvalues and then obtain comparisons of these smallest eigenvalues as functions of
both p and β.
denote standard
Riemann-Liouville differential operators. We prove the existence of smallest positive
eigenvalues and then obtain comparisons of these smallest eigenvalues as functions of
both p and β.
Submitted October 14, 2020. Published July 7, 2021.
Math Subject Classifications: 26A33, 34A08, 34A40, 26D20
Key Words: Riemann-Liouville fractional differential equation;
boundary value problem; principal eigenvalue; fractional boundary conditions
DOI: https://doi.org/10.58997/ejde.2021.62
Show me the PDF file (342 KB),
TEX file for this article.
 |
Paul W. Eloe
Department of Mathematics
University of Dayton
Dayton, OH 45469, USA
email: peloe1@udayton.edu
|
|---|
 |
Jeffrey T. Neugebauer
Department of Mathematics and Statistics
Eastern Kentucky University
Richmond, KY 40475, USA
email: Jeffrey.Neugebauer@eku.edu
|
|---|
Return to the EJDE web page

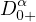 and
and
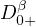 denote standard
Riemann-Liouville differential operators. We prove the existence of smallest positive
eigenvalues and then obtain comparisons of these smallest eigenvalues as functions of
both p and β.
denote standard
Riemann-Liouville differential operators. We prove the existence of smallest positive
eigenvalues and then obtain comparisons of these smallest eigenvalues as functions of
both p and β.

