Electron. J. Differential Equations, Vol. 2021 (2021), No. 66, pp. 1-20.
Multiplicity and asymptotic behavior of solutions to fractional (p,q)-Kirchhoff
type problems with critical Sobolev-Hardy exponent
Xiaolu Lin, Shenzhou Zheng
Abstract:
Let
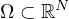 be a bounded domain with smooth boundary and
be a bounded domain with smooth boundary and
 .
For 0<s<1, 1≤r<q<p, 0≤α<ps<N and a positive parameter λ, we consider
the fractional (p,q)-Laplacian problems involving a critical Sobolev-Hardy exponent.
This model comes from a nonlocal problem of Kirchhoff type
.
For 0<s<1, 1≤r<q<p, 0≤α<ps<N and a positive parameter λ, we consider
the fractional (p,q)-Laplacian problems involving a critical Sobolev-Hardy exponent.
This model comes from a nonlocal problem of Kirchhoff type
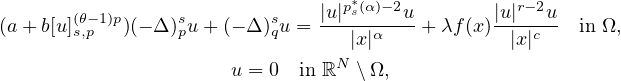
where a,b>0, c<sr+N(1-r/p),
 and
and
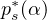 is critical Sobolev-Hardy exponent.
For a given suitable f(x), we prove that there are least two nontrivial
solutions for small λ, by way of the mountain pass theorem and Ekeland's variational
principle. Furthermore, we prove that these two solutions converge to two solutions
of the limiting problem as
is critical Sobolev-Hardy exponent.
For a given suitable f(x), we prove that there are least two nontrivial
solutions for small λ, by way of the mountain pass theorem and Ekeland's variational
principle. Furthermore, we prove that these two solutions converge to two solutions
of the limiting problem as
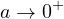 .
For the limiting problem, we show the existence
of infinitely many solutions, and the sequence tends to zero when λ
belongs to a suitable range.
.
For the limiting problem, we show the existence
of infinitely many solutions, and the sequence tends to zero when λ
belongs to a suitable range.
Submitted January 12, 2021. Published August 10, 2021.
Math Subject Classifications: 35A15, 35B33, 35R11.
Key Words: Fractional (p,q)-Kirchhoff operators; critical Sobolev-Hardy exponent;
multiple solutions; asymptotic behavior; symmetric mountain pass lemma.
DOI: https://doi.org/10.58997/ejde.2021.66
Show me the PDF file (440 KB),
TEX file for this article.
 |
Xiaolu Lin
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: 19118003@bjtu.edu.cn
|
|---|
 |
Shenzhou Zheng
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: shzhzheng@bjtu.edu.cn
|
|---|
Return to the EJDE web page
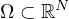 be a bounded domain with smooth boundary and
be a bounded domain with smooth boundary and
 .
For 0<s<1, 1≤r<q<p, 0≤α<ps<N and a positive parameter λ, we consider
the fractional (p,q)-Laplacian problems involving a critical Sobolev-Hardy exponent.
This model comes from a nonlocal problem of Kirchhoff type
.
For 0<s<1, 1≤r<q<p, 0≤α<ps<N and a positive parameter λ, we consider
the fractional (p,q)-Laplacian problems involving a critical Sobolev-Hardy exponent.
This model comes from a nonlocal problem of Kirchhoff type
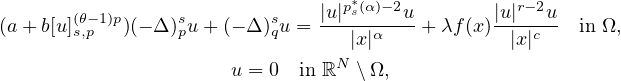
 and
and
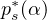 is critical Sobolev-Hardy exponent.
For a given suitable f(x), we prove that there are least two nontrivial
solutions for small λ, by way of the mountain pass theorem and Ekeland's variational
principle. Furthermore, we prove that these two solutions converge to two solutions
of the limiting problem as
is critical Sobolev-Hardy exponent.
For a given suitable f(x), we prove that there are least two nontrivial
solutions for small λ, by way of the mountain pass theorem and Ekeland's variational
principle. Furthermore, we prove that these two solutions converge to two solutions
of the limiting problem as
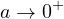 .
For the limiting problem, we show the existence
of infinitely many solutions, and the sequence tends to zero when λ
belongs to a suitable range.
.
For the limiting problem, we show the existence
of infinitely many solutions, and the sequence tends to zero when λ
belongs to a suitable range.

