Electron. J. Differential Equations, Vol. 2021 (2021), No. 75, pp. 1-26.
Nonexistence results for hyperbolic type inequalities involving the
Grushin operator in exterior domains
Mohamed Jleli, Bessem Samet
Abstract:
We study the hyperbolic type differential inequality
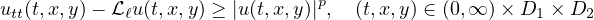
under the boundary conditions
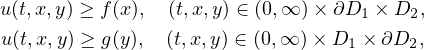
where
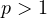 ,
,
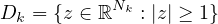 ,
,
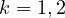 ,
,
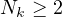 ,
,
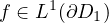 ,
,
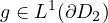 , and
, and
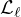 ,
,
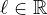 , is the Grushin operator
, is the Grushin operator
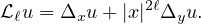
We obtain sufficient conditions depending on
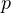 ,
,
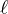 ,
,
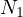 ,
,
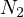 ,
,
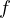 , and
, and
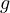 ,
for which the considered problem admits no global weak solution.
We discuss separately the four cases:
,
for which the considered problem admits no global weak solution.
We discuss separately the four cases:
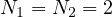 ;
;
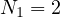 ,
,
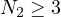 ;
;
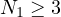 ,
,
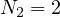 ;
;
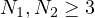 .
.
Submitted June 25, 2021. Published September 14, 2021.
Math Subject Classifications: 35B44, 35B33, 35L10.
Key Words: Global weak solutions; hyperbolic type inequalities; exterior domain;
Grushin operator.
DOI: https://doi.org/10.58997/ejde.2021.75
Show me the PDF file (413 KB),
TEX file for this article.
 |
Mohamed Jleli
Department of Mathematics
College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: jleli@ksu.edu.sa
|
|---|
 |
Bessem Samet
Department of Mathematics
College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: bsamet@ksu.edu.sa
|
|---|
Return to the EJDE web page
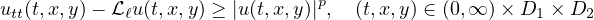
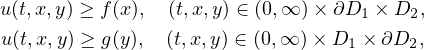
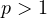 ,
,
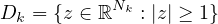 ,
,
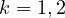 ,
,
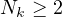 ,
,
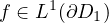 ,
,
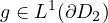 , and
, and
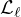 ,
,
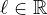 , is the Grushin operator
, is the Grushin operator
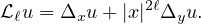
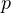 ,
,
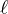 ,
,
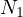 ,
,
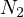 ,
,
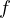 , and
, and
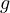 ,
for which the considered problem admits no global weak solution.
We discuss separately the four cases:
,
for which the considered problem admits no global weak solution.
We discuss separately the four cases:
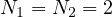 ;
;
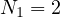 ,
,
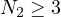 ;
;
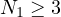 ,
,
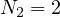 ;
;
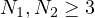 .
.

