Electron. J. Differential Equations, Vol. 2021 (2021), No. 92, pp. 1-20.
Lower order for meromorphic solutions to linear delay-differential equations
Rachid Bellaama, Benharrat Belaidi
Abstract:
In this article, we study the order of growth for solutions of
the non-homogeneous linear delay-differential equation
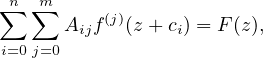
where
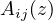
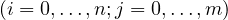 ,
,
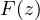 are entire or meromorphic functions and
are entire or meromorphic functions and
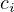
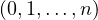 are non-zero distinct complex numbers. Under the
condition that there exists one coefficient having the maximal
lower order, or having the maximal lower type, strictly greater than
the order, or the type, of the other coefficients,
we obtain estimates of the lower bound of the order of meromorphic solutions
of the above equation.
are non-zero distinct complex numbers. Under the
condition that there exists one coefficient having the maximal
lower order, or having the maximal lower type, strictly greater than
the order, or the type, of the other coefficients,
we obtain estimates of the lower bound of the order of meromorphic solutions
of the above equation.
Submitted June 25, 2021. Published November 18, 2021.
Math Subject Classifications: 30D35, 39B32, 39A10.
Key Words: Linear difference equation; linear delay-differential equation;
meromorphic solution; order; type; lower order, lower type.
DOI: https://doi.org/10.58997/ejde.2021.92
Show me the PDF file (356 KB),
TEX file for this article.
 |
Rachid Bellaama
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem, Algeria
email: rachidbellaama10@gmail.com
|
|---|
 |
Benharrat Belaïdi
Department of Mathematics
Laboratory of Pure and Applied Mathematics
University of Mostaganem, Algeria
email: benharrat.belaidi@univ-mosta.dz
|
|---|
Return to the EJDE web page
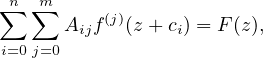
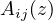
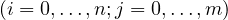 ,
,
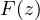 are entire or meromorphic functions and
are entire or meromorphic functions and
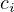
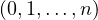 are non-zero distinct complex numbers. Under the
condition that there exists one coefficient having the maximal
lower order, or having the maximal lower type, strictly greater than
the order, or the type, of the other coefficients,
we obtain estimates of the lower bound of the order of meromorphic solutions
of the above equation.
are non-zero distinct complex numbers. Under the
condition that there exists one coefficient having the maximal
lower order, or having the maximal lower type, strictly greater than
the order, or the type, of the other coefficients,
we obtain estimates of the lower bound of the order of meromorphic solutions
of the above equation.

