Electron. J. Differential Equations, Vol. 2022 (2022), No. 01, pp. 1-13.
Positive solutions for a class of phi-Laplacian differential systems with multiple parameters
Xiaozhu Yu, Shiwen Jing, Hairong Lian
Abstract:
In this article, we consider the double eigenvalue problem for a
φ-Laplacian differential system.
We prove the existence of positive solutions under the φ-super-linear condition
by means of the Guo-Krasnosel'skii fixed point theorem and the topological degree.
It is shown that there exists a continuous curve splitting
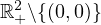 into disjoint subsets such that systems has at least two, at least one, or no positive
solutions according to parameters in different subsets.
into disjoint subsets such that systems has at least two, at least one, or no positive
solutions according to parameters in different subsets.
Submitted August 27, 2021. Published January 5, 2022.
Math Subject Classifications: 34B16, 34L15.
Key Words: phi-Laplacian differential systems; eigenvalue; fixed point theorem;
degree theory; positive solution.
DOI: https://doi.org/10.58997/ejde.2022.01
Show me the PDF file (348 KB),
TEX file for this article.
 |
Xiaozhu Yu
School of Science
China University of Geosciences
Beijing 100083, China
email: yuxiaozhu@cugb.edu.cn
|
|---|
 |
Shiwen Jing
School of Science
China University of Geosciences
Beijing 100083, China
email: 2019210011@email.cugb.edu.cn
|
|---|
 |
Hairong Lian
School of Science
China University of Geosciences
Beijing 100083, China
email: lianhr@126.com
|
|---|
Return to the EJDE web page
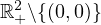 into disjoint subsets such that systems has at least two, at least one, or no positive
solutions according to parameters in different subsets.
into disjoint subsets such that systems has at least two, at least one, or no positive
solutions according to parameters in different subsets.


