Electron. J. Differential Equations, Vol. 2022 (2022), No. 07, pp. 1-18.
Asymptotic behavior of solutions to 3D Kelvin-Voigt-Brinkman-Forchheimer
equations with unbounded delays
Le Thi Thuy
Abstract:
In this article we consider a 3D Kelvin Voigt Brinkman Forchheimer equations
involving unbounded delays in a bounded domain
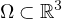 .
First, we show the existence and uniqueness of weak solutions by using the
Galerkin approximations method and the energy method.
Second, we prove the existence and uniqueness of stationary solutions by employing
the Brouwer fixed point theorem. Finally, we study the stability of stationary solutions
via the direct classical approach and the construction of a Lyapunov function.
We also give a sufficient condition for the polynomial stability of the stationary
solution for a special case of unbounded variable delay.
.
First, we show the existence and uniqueness of weak solutions by using the
Galerkin approximations method and the energy method.
Second, we prove the existence and uniqueness of stationary solutions by employing
the Brouwer fixed point theorem. Finally, we study the stability of stationary solutions
via the direct classical approach and the construction of a Lyapunov function.
We also give a sufficient condition for the polynomial stability of the stationary
solution for a special case of unbounded variable delay.
Submitted November 3, 2020. Published January 17, 2022.
Math Subject Classifications: 35B41, 35K65, 35D05
Key Words: Kelvin-Voigt-Brinkman-Forchheimer equation; delay equation;
stationary solution; local stability; asymptotically stable; polynomial stable.
DOI: https://doi.org/10.58997/ejde.2022.07
Show me the PDF file (364 KB),
TEX file for this article.
 |
Le Thi Thuy
Department of Mathematics
Electric Power University
235, Hoang Quoc Viet
Bac Tu Liem, Hanoi, Vietnam
email: thuylt@epu.edu.vn, thuylephuong@gmail.com
|
Return to the EJDE web page
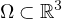 .
First, we show the existence and uniqueness of weak solutions by using the
Galerkin approximations method and the energy method.
Second, we prove the existence and uniqueness of stationary solutions by employing
the Brouwer fixed point theorem. Finally, we study the stability of stationary solutions
via the direct classical approach and the construction of a Lyapunov function.
We also give a sufficient condition for the polynomial stability of the stationary
solution for a special case of unbounded variable delay.
.
First, we show the existence and uniqueness of weak solutions by using the
Galerkin approximations method and the energy method.
Second, we prove the existence and uniqueness of stationary solutions by employing
the Brouwer fixed point theorem. Finally, we study the stability of stationary solutions
via the direct classical approach and the construction of a Lyapunov function.
We also give a sufficient condition for the polynomial stability of the stationary
solution for a special case of unbounded variable delay.
