Electron. J. Differential Equations, Vol. 2022 (2022), No. 08, pp. 1-17.
Blow-up for parabolic equations in nonlinear divergence form with time-dependent coefficients
Xuhui Shen, Juntang Ding
Abstract:
In this article, we study the blow-up of solutions to the nonlinear parabolic equation
in divergence form,
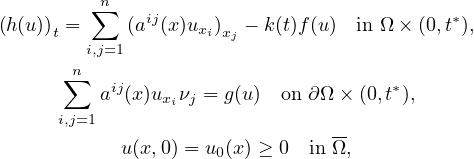
where
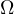 is a bounded convex domain in
is a bounded convex domain in

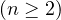 with
smooth boundary
with
smooth boundary
 . By constructing suitable auxiliary functions
and using a differential inequality technique, when
. By constructing suitable auxiliary functions
and using a differential inequality technique, when
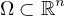
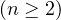 , we establish conditions for the solution blow up at a finite time,
and conditions for the solution to exist for all time.
Also, we find an upper bound for the blow-up time.
In addition, when
, we establish conditions for the solution blow up at a finite time,
and conditions for the solution to exist for all time.
Also, we find an upper bound for the blow-up time.
In addition, when
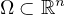 with
with
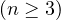 , we use a
Sobolev inequality to obtain a lower bound for the blow-up time.
, we use a
Sobolev inequality to obtain a lower bound for the blow-up time.
Submitted January 27, 2021. Published January 25, 2022.
Math Subject Classifications: 35K55, 35B44.
Key Words: Nonlinear parabolic equation; blow-up; upper bound; lower bound.
DOI: https://doi.org/10.58997/ejde.2022.08
Show me the PDF file (373 KB),
TEX file for this article.
 |
Xuhui Shen
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: xhuishen@163.com
|
|---|
 |
Juntang Ding
School of Mathematical Sciences
Shanxi University
Taiyuan 030006, China
email: djuntang@sxu.edu.cn
|
|---|
Return to the EJDE web page
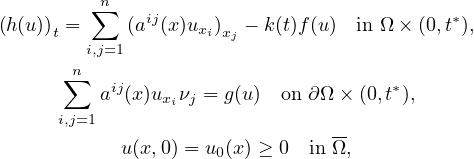
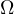 is a bounded convex domain in
is a bounded convex domain in

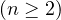 with
smooth boundary
with
smooth boundary
 . By constructing suitable auxiliary functions
and using a differential inequality technique, when
. By constructing suitable auxiliary functions
and using a differential inequality technique, when
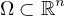
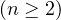 , we establish conditions for the solution blow up at a finite time,
and conditions for the solution to exist for all time.
Also, we find an upper bound for the blow-up time.
In addition, when
, we establish conditions for the solution blow up at a finite time,
and conditions for the solution to exist for all time.
Also, we find an upper bound for the blow-up time.
In addition, when
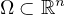 with
with
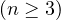 , we use a
Sobolev inequality to obtain a lower bound for the blow-up time.
, we use a
Sobolev inequality to obtain a lower bound for the blow-up time.

