Electron. J. Differential Equations, Vol. 2022 (2022), No. 09, pp. 1-13.
Existence of global weak solutions for a p-Laplacian inequality with strong dissipation in noncylindrical domains
Jorge Ferreira, Erhan Piskin, Mohammad Shahrouzi, Sebastiao Cordeiro, Carlos Alberto Raposo
Abstract:
In this work, we obtain global solutions for nonlinear inequalities of
p-Laplacian type in noncylindrical domains, for the unilateral problem
with strong dissipation
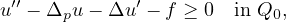
where
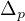 is the nonlinear p-Laplacian operator with
is the nonlinear p-Laplacian operator with
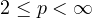 , and
, and
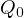 is the noncylindrical domain.
Our proof is based on a penalty argument by J. L. Lions and Faedo-Galerkin approximations
is the noncylindrical domain.
Our proof is based on a penalty argument by J. L. Lions and Faedo-Galerkin approximations
Submitted February 4, 2021. Published January 27, 2022.
Math Subject Classifications: 35Q55, 35B44, 26A33, 35B30.
Key Words: Global solution; weak solutions; p-Laplacian inequality;
strong dissipation; noncylindrical domain.
DOI: https://doi.org/10.58997/ejde.2022.09
Show me the PDF file (355 KB),
TEX file for this article.
 |
Jorge Ferreira
Department of Exact Sciences
Federal Fluminense University
Volta Redonda, 27213-145 RJ, Brazil
email: jorge_ferreira@id.uff.br
|
|---|
 |
Erhan Pişkin
Department of Mathematics
Dicle University
Diyarbakir, Turkey
email: episkin@dicle.edu.tr
|
|---|
 |
Mohammad Shahrouzi
Department of Mathematics
Jahrom University
Jahrom, P.O. Box: 74137-66171, Iran
email: mshahrouzi@jahromu.ac.ir
|
|---|
 |
Sebastião Cordeiro
Faculty of Exact Sciences and Technology
Federal University of Pará
Abaetetuba, 68440-000 PA, Brazil
email: sebastiao@ufpa.br
|
|---|
 |
Carlos Alberto Raposo
Department of Mathematics and Statistics
Federal University of São João del-Rei
São João del-Rei, 36307-352 MG, Brazil
email: raposo@ufsj.edu.br
|
|---|
Return to the EJDE web page
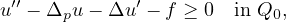
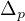 is the nonlinear p-Laplacian operator with
is the nonlinear p-Laplacian operator with
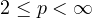 , and
, and
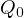 is the noncylindrical domain.
Our proof is based on a penalty argument by J. L. Lions and Faedo-Galerkin approximations
is the noncylindrical domain.
Our proof is based on a penalty argument by J. L. Lions and Faedo-Galerkin approximations




