Electron. J. Differential Equations, Vol. 2022 (2022), No. 11, pp. 1-29.
Localized nodal solutions for semiclassical quasilinear Choquard equations with subcritical growth
Bo Zhang, Xiangqing Liu
Abstract:
In this article, we study the existence of localized nodal solutions for semiclassical
quasilinear Choquard equations with subcritical growth

where
 ,
,
 ,
,
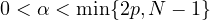 ,
,
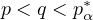 ,
,
 , V is a bounded function.
By the perturbation method and the method of invariant sets of descending flow,
for small
, V is a bounded function.
By the perturbation method and the method of invariant sets of descending flow,
for small
 we establish the existence of a sequence of localized nodal
solutions concentrating near a given local minimum point of the potential function V.
we establish the existence of a sequence of localized nodal
solutions concentrating near a given local minimum point of the potential function V.
Submitted September 6, 2021. Published February 10, 2022.
Math Subject Classifications: 35B20, 35B40.
Key Words: Quasilinear Choquard equation; nodal solutions; perturbation method.
DOI: https://doi.org/10.58997/ejde.2022.11
Show me the PDF file (459 KB),
TEX file for this article.
| |
Bo Zhang
Department of Mathematics
Yunnan Normal University
Kunming, Yunnan 650500, China
email: zhangbo371013@163.com
|
|---|
 |
Xiangqing Liu
Department of Mathematics
Yunnan Normal University
Kunming, Yunnan 650500, China
email: lxq8u8@163.com
|
|---|
Return to the EJDE web page

 ,
,
 ,
,
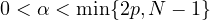 ,
,
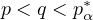 ,
,
 , V is a bounded function.
By the perturbation method and the method of invariant sets of descending flow,
for small
, V is a bounded function.
By the perturbation method and the method of invariant sets of descending flow,
for small
 we establish the existence of a sequence of localized nodal
solutions concentrating near a given local minimum point of the potential function V.
we establish the existence of a sequence of localized nodal
solutions concentrating near a given local minimum point of the potential function V.
