Electron. J. Differential Equations, Vol. 2022 (2022), No. 13, pp. 1-12.
Remarks on the second Neumann eigenvalue
Jose C. Sabina de Lis
Abstract:
This work reviews some basic features on the second (first nontrivial) eigenvalue
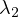 to the Neumann problem
to the Neumann problem
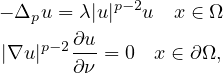
where
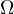 is a bounded Lipschitz domain of
is a bounded Lipschitz domain of
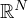 ,
,
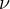 is the
outer unit normal, and
is the
outer unit normal, and
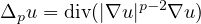 is the p-Laplacian operator. We are mainly concerned with the
variational characterization of
is the p-Laplacian operator. We are mainly concerned with the
variational characterization of
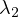 and place emphasis on the range
1 < p < 2, where the nonlinearity
and place emphasis on the range
1 < p < 2, where the nonlinearity
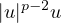 becomes non smooth.
We also address the corresponding result for the p-Laplacian in graphs.
becomes non smooth.
We also address the corresponding result for the p-Laplacian in graphs.
Submitted August 16, 2021. Published February 20, 2022.
Math Subject Classifications: 35J70, 35J92, 35P30.
Key Words: p-Laplacian operator; eigenvalues; Neumann conditions.
DOI: https://doi.org/10.58997/ejde.2022.13
Show me the PDF file (362 KB),
TEX file for this article.
 |
José C. Sabina de Lis
Departamento de Análisis Matemático and IUEA
Universidad de La Laguna
C. Astrofísico Francisco Sánchez s/n, 38203
La Laguna, Spain
email: josabina@ull.edu.es
|
|---|
Return to the EJDE web page
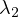 to the Neumann problem
to the Neumann problem
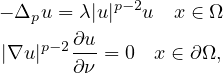
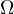 is a bounded Lipschitz domain of
is a bounded Lipschitz domain of
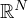 ,
,
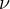 is the
outer unit normal, and
is the
outer unit normal, and
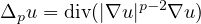 is the p-Laplacian operator. We are mainly concerned with the
variational characterization of
is the p-Laplacian operator. We are mainly concerned with the
variational characterization of
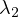 and place emphasis on the range
1 < p < 2, where the nonlinearity
and place emphasis on the range
1 < p < 2, where the nonlinearity
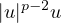 becomes non smooth.
We also address the corresponding result for the p-Laplacian in graphs.
becomes non smooth.
We also address the corresponding result for the p-Laplacian in graphs.
