Electron. J. Differential Equations, Vol. 2022 (2022), No. 42, pp. 1-19.
Asymptotic behavior of blowup solutions for Henon type parabolic equations with exponential nonlinearity
Caihong Chang, Zhengce Zhang
Abstract:
This article concerns the blow up behavior for the Henon type parabolic equation with
exponential nonlinearity,

where
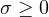 and
and
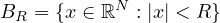 .
We consider all cases in which blowup of solutions occurs, i.e.
.
We consider all cases in which blowup of solutions occurs, i.e.
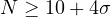 .
Grow up rates are established by a certain matching of different asymptotic behaviors
in the inner region (near the singularity) and the outer region (close to the boundary).
For the cases
.
Grow up rates are established by a certain matching of different asymptotic behaviors
in the inner region (near the singularity) and the outer region (close to the boundary).
For the cases
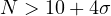 and
and
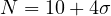 , the asymptotic expansions of stationary
solutions have different forms, so two cases are discussed separately. Moreover, different
inner region widths in two cases are also obtained.
, the asymptotic expansions of stationary
solutions have different forms, so two cases are discussed separately. Moreover, different
inner region widths in two cases are also obtained.
Submitted May 3, 2021. Published June 28, 2022.
Math Subject Classifications: 35A01, 35B40, 35B44, 35K20.
Key Words: Matched expansion; weighted term; stabilization; grow up rate; degeneracy.
DOI: https://doi.org/10.58997/ejde.2022.42
Show me the PDF file (403 KB),
TEX file for this article.
 |
Caihong Chang
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an, 710049, China
email: caihong666@stu.xjtu.edu.cn
|
|---|
 |
Zhengce Zhang
School of Mathematics and Statistics
Xi'an Jiaotong University
Xi'an, 710049, China
email: zhangzc@mail.xjtu.edu.cn
|
|---|
Return to the EJDE web page

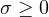 and
and
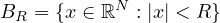 .
We consider all cases in which blowup of solutions occurs, i.e.
.
We consider all cases in which blowup of solutions occurs, i.e.
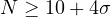 .
Grow up rates are established by a certain matching of different asymptotic behaviors
in the inner region (near the singularity) and the outer region (close to the boundary).
For the cases
.
Grow up rates are established by a certain matching of different asymptotic behaviors
in the inner region (near the singularity) and the outer region (close to the boundary).
For the cases
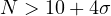 and
and
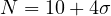 , the asymptotic expansions of stationary
solutions have different forms, so two cases are discussed separately. Moreover, different
inner region widths in two cases are also obtained.
, the asymptotic expansions of stationary
solutions have different forms, so two cases are discussed separately. Moreover, different
inner region widths in two cases are also obtained.

