Electron. J. Differential Equations, Vol. 2022 (2022), No. 47, pp. 1-21.
Multiplicity of high energy solutions for fractional Schrodinger-Poisson systems with critical frequency
Siqi Qu, Xiaoming He
Abstract:
In this article we study the fractional Schrodinger-Poisson system
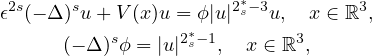
where
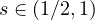 ,
,
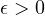 is a parameter,
is a parameter,
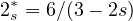 is the critical Sobolev exponent,
is the critical Sobolev exponent,
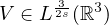 is a nonnegative function which may be zero in some region of
is a nonnegative function which may be zero in some region of
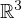 .
By means of variational methods, we present the number of high energy bound states
with the topology of the zero set of V for small
.
By means of variational methods, we present the number of high energy bound states
with the topology of the zero set of V for small
 .
.
Submitted March 11, 2022. Published July 5, 2022.
Math Subject Classifications: 35B35, 35B40, 35K57, 35Q92, 92C17.
Key Words: Fractional Schrodinger-Poisson system; high energy solution; critical Sobolev exponent.
DOI: https://doi.org/10.58997/ejde.2022.47
Show me the PDF file (418 KB),
TEX file for this article.
 |
Siqi Qu
College of Science
Minzu University of China
Beijing, 100081, China
email: qusiqi78@gmail.com
|
|---|
 |
Xiaoming He
College of Science
Minzu University of China
Beijing, 100081, China
email: xmhe923@muc.edu.cn
|
|---|
Return to the EJDE web page
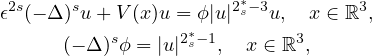
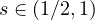 ,
,
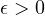 is a parameter,
is a parameter,
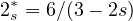 is the critical Sobolev exponent,
is the critical Sobolev exponent,
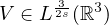 is a nonnegative function which may be zero in some region of
is a nonnegative function which may be zero in some region of
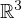 .
By means of variational methods, we present the number of high energy bound states
with the topology of the zero set of V for small
.
By means of variational methods, we present the number of high energy bound states
with the topology of the zero set of V for small
 .
.

