Electron. J. Differential Equations, Vol. 2022 (2022), No. 57, pp. 1-23.
Localized nodal solutions for semiclassical nonlinear Kirchhoff equations
Lixia Wang
Abstract:
In this article, we consider the existence of localized sign-changing solutions
for the semiclassical Kirchhoff equation
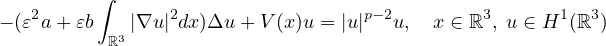
where
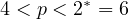 ,
,
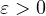 is a small parameter,
V(x) is a positive function that has a local minimum point P.
When
is a small parameter,
V(x) is a positive function that has a local minimum point P.
When
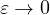 , by using a minimax characterization of higher
dimensional symmetric linking structure via the symmetric mountain pass theorem,
we obtain an infinite sequence of localized sign-changing solutions
clustered at the point P.
, by using a minimax characterization of higher
dimensional symmetric linking structure via the symmetric mountain pass theorem,
we obtain an infinite sequence of localized sign-changing solutions
clustered at the point P.
Submitted April 18, 2022. Published August 2, 2022.
Math Subject Classifications: 35J20, 35J60.
Key Words: Kirchhoff equations; nodal solutions; penalization method.
Show me the PDF file (419 KB),
TEX file for this article.
DOI: https://doi.org/10.58997/ejde.2022.57
 |
Lixia Wang
School of Sciences
Tianjin Chengjian University
Tianjin 300384, China
email: wanglixia0311@126.com
|
|---|
Return to the EJDE web page
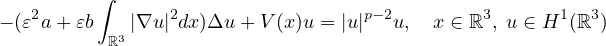
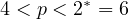 ,
,
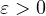 is a small parameter,
V(x) is a positive function that has a local minimum point P.
When
is a small parameter,
V(x) is a positive function that has a local minimum point P.
When
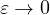 , by using a minimax characterization of higher
dimensional symmetric linking structure via the symmetric mountain pass theorem,
we obtain an infinite sequence of localized sign-changing solutions
clustered at the point P.
, by using a minimax characterization of higher
dimensional symmetric linking structure via the symmetric mountain pass theorem,
we obtain an infinite sequence of localized sign-changing solutions
clustered at the point P.
