Electron. J. Differential Equations, Vol. 2022 (2022), No. 58, pp. 1-17.
Boundedness and asymptotic stability in a chemotaxis model with indirect signal production and logistic source
Xiaobing Ye, Liangchen Wang
Abstract:
This article concerns the chemotaxis-growth system with indirect signal production
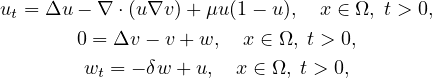
on a smooth bounded domain
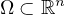 (
(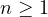 ) with homogeneous
Neumann boundary condition, where the parameters
) with homogeneous
Neumann boundary condition, where the parameters
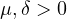 .
It is proved that if
.
It is proved that if
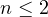 and
and
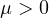 ,
for all suitably regular initial data,
this model possesses a unique global classical solution which is uniformly-in-time
bounded. While in the case
,
for all suitably regular initial data,
this model possesses a unique global classical solution which is uniformly-in-time
bounded. While in the case
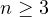 ,
we show that if
,
we show that if
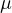 is sufficiently large,
this system possesses a global bounded solution.
Furthermore, the large time behavior and rates of convergence have also been considered
under some explicit conditions.
is sufficiently large,
this system possesses a global bounded solution.
Furthermore, the large time behavior and rates of convergence have also been considered
under some explicit conditions.
Submitted February 15, 2021. Published August 2, 2022.
Math Subject Classifications: 92C17, 35K35, 35A01, 35B35.
Key Words: Chemotaxis; boundedness; asymptotic behavior; indirect signal production.
DOI: https://doi.org/10.58997/ejde.2022.58
Show me the PDF file (372 KB),
TEX file for this article.
 |
Xiaobing Ye
School of Science
Chongqing University of Posts and Telecommunications
Chongqing 400065, China
email: xiaobingye1130@126.com
|
|---|
 |
Liangchen Wang
School of Science
Chongqing University of Posts and Telecommunications
Chongqing 400065, China
email: wanglc@cqupt.edu.cn
|
|---|
Return to the EJDE web page
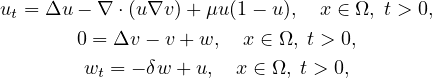
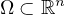 (
(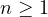 ) with homogeneous
Neumann boundary condition, where the parameters
) with homogeneous
Neumann boundary condition, where the parameters
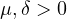 .
It is proved that if
.
It is proved that if
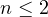 and
and
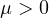 ,
for all suitably regular initial data,
this model possesses a unique global classical solution which is uniformly-in-time
bounded. While in the case
,
for all suitably regular initial data,
this model possesses a unique global classical solution which is uniformly-in-time
bounded. While in the case
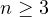 ,
we show that if
,
we show that if
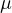 is sufficiently large,
this system possesses a global bounded solution.
Furthermore, the large time behavior and rates of convergence have also been considered
under some explicit conditions.
is sufficiently large,
this system possesses a global bounded solution.
Furthermore, the large time behavior and rates of convergence have also been considered
under some explicit conditions.

