Electron. J. Differential Equations, Vol. 2022 (2022), No. 60, pp. 1-19.
Topological structure of the solution set for a fractional p-Laplacian problem
with singular nonlinearity
Marcos R. Marcial, Olimpio H. Miyagaki, Gilberto A. Pereira
Abstract:
We establish the existence of connected components of positive solutions for the
equation
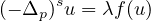 , under Dirichlet boundary conditions,
where the domain is a bounded in
, under Dirichlet boundary conditions,
where the domain is a bounded in
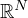 and has
smooth boundary,
and has
smooth boundary,
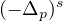 is the fractional p-Laplacian operator,
and
is the fractional p-Laplacian operator,
and
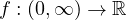 is a continuous function which may blow
up to
is a continuous function which may blow
up to
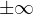 at the origin.
at the origin.
Submitted December 8, 2021. Published August 11, 2022.
Math Subject Classifications: 35A16, 35B65, 35J75, 35J92.
Key Words: Monotonicity methods; singular problems; regularity;
fractional p-laplacian operator.
DOI: https://doi.org/10.58997/ejde.2022.60
An addendum was posted on August 19, 2022. It expands Remark 2.1 and add 3 references. See the last page of this article.
Show me the PDF file (382 KB),
TEX file for this article.
 |
Marcos Roberto Marcial
Universidade Federal de Ouro Preto
Departamento de Matemática
35400-000 - Ouro Preto - MG, Brazil
email: mrmarcial@ufop.edu.br
|
|---|
 |
Olimpio H. Miyagaki
Departmento de Matemática
Universidade Federal de São Carlos
13565-905 - São Carlos - SP, Brazil
email: olimpio@ufscar.br, ohmiyagaki@gmail.com
|
|---|
 |
Gilberto A. Pereira
Universidade Federal de Ouro Preto
Departamento de Matemática
35400-000 - Ouro Preto - MG, Brazil
email: gilberto.pereira@ufop.edu.br
|
|---|
Return to the EJDE web page
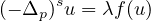 , under Dirichlet boundary conditions,
where the domain is a bounded in
, under Dirichlet boundary conditions,
where the domain is a bounded in
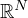 and has
smooth boundary,
and has
smooth boundary,
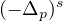 is the fractional p-Laplacian operator,
and
is the fractional p-Laplacian operator,
and
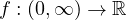 is a continuous function which may blow
up to
is a continuous function which may blow
up to
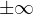 at the origin.
at the origin.


