Electron. J. Differential Equations, Vol. 2022 (2022), No. 61, pp. 1-14.
Ground state solutions for fractional p-Kirchhoff equation
Lixiong Wang, Haibo Chen, Liu Yang
Abstract:
We study the fractional p-Kirchhoff equation
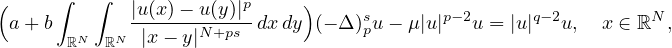
where
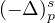 is the fractional p-Laplacian operator, a and b are strictly
positive real numbers,
is the fractional p-Laplacian operator, a and b are strictly
positive real numbers,
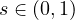 ,
,
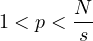 , and
, and
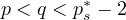 with
with
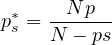 . By using the variational method, we prove the existence
and uniqueness of global minimum or mountain pass type critical points on the
. By using the variational method, we prove the existence
and uniqueness of global minimum or mountain pass type critical points on the
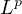 -normalized manifold
-normalized manifold
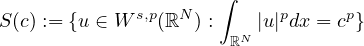 .
.
Submitted April 11, 2022. Published August 19, 2022.
Math Subject Classifications: 35J20, 35J60.
Key Words: Variational method; L^p-normalized critical point; fractional;
p-Kirchhoff equation; uniqueness.
DOI: https://doi.org/10.58997/ejde.2022.61
Show me the PDF file (383 KB),
TEX file for this article.
 |
Lixiong Wang
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: wanglixiong2018@163.com
|
|---|
 |
Haibo Chen
School of Mathematics and Statistics
Central South University
Changsha, 410083 Hunan, China
email: math_chb@163.com
|
|---|
 |
Liu Yang
College of Mathematics and Statistics
Hengyang Normal University
Hengyang, 421008 Hunan, China
email: yangliuyanzi@163.com
|
|---|
Return to the EJDE web page
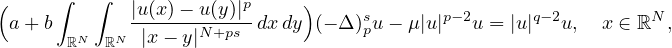
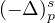 is the fractional p-Laplacian operator, a and b are strictly
positive real numbers,
is the fractional p-Laplacian operator, a and b are strictly
positive real numbers,
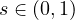 ,
,
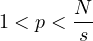 , and
, and
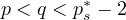 with
with
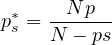 . By using the variational method, we prove the existence
and uniqueness of global minimum or mountain pass type critical points on the
. By using the variational method, we prove the existence
and uniqueness of global minimum or mountain pass type critical points on the
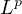 -normalized manifold
-normalized manifold
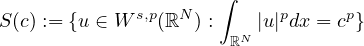 .
.


