Electron. J. Differential Equations, Vol. 2022 (2022), No. 63, pp. 1-25.
Solvability of inclusions involving perturbations of positively homogeneous maximal monotone operators
Dhruba R. Adhikari, Ashok Aryal, Ghanshyam Bhatt, Ishwari J. Kunwar, Rajan Puri, Min Ranabhat
Abstract:
Let
 be a real reflexive Banach space and
be a real reflexive Banach space and
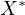 be its dual space.
Let
be its dual space.
Let
 and
and
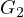 be open subsets of
be open subsets of
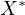 such that
such that
 ,
,
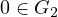 , and
, and
 is bounded.
Let
is bounded.
Let
 be a densely defined linear maximal
monotone operator,
be a densely defined linear maximal
monotone operator,
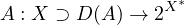 be a maximal monotone and positively
homogeneous operator of degree
be a maximal monotone and positively
homogeneous operator of degree
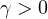 ,
,
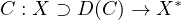 be a bounded
demicontinuous operator of type
be a bounded
demicontinuous operator of type
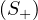 with respect to
with respect to
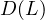 , and
, and
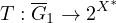 be a compact and upper-semicontinuous operator whose values
are closed and convex sets in
be a compact and upper-semicontinuous operator whose values
are closed and convex sets in
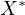 .
We first take
.
We first take
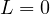 and establish the existence of nonzero solutions of
and establish the existence of nonzero solutions of
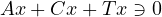 in the set
in the set
 .
Secondly, we assume that
.
Secondly, we assume that
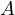 is bounded and establish the existence of nonzero solutions
of
is bounded and establish the existence of nonzero solutions
of
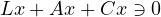 in
in
 .
We remove the restrictions
.
We remove the restrictions
![$\gamma\in (0, 1]$](images/a19x.png) for
for
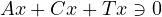 and
and
 for
for
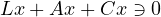 from such existing results in the literature.
We also present applications to elliptic and parabolic partial differential equations
in general divergence form satisfying Dirichlet boundary conditions.
from such existing results in the literature.
We also present applications to elliptic and parabolic partial differential equations
in general divergence form satisfying Dirichlet boundary conditions.
Submitted April 1, 2022. Published August 30, 2022.
Math Subject Classifications: 47H14, 47H05, 47H11.
Key Words: Topological degree theory; operators of type
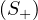 ;
monotone operator; duality mapping; Yosida approximant.
;
monotone operator; duality mapping; Yosida approximant.
DOI: https://doi.org/10.58997/ejde.2022.63
Show me the PDF file (448 KB),
TEX file for this article.
 |
Dhruba R. Adhikari
Department of Mathematics
Kennesaw State University
Marietta, GA 30060, USA
email: dadhikar@kennesaw.edu
|
|---|
 |
Ashok Aryal
Mathematics Department
Minnesota State University Moorhead
Moorhead, MN 56563, USA
email: ashok.aryal@mnstate.edu
|
|---|
 |
Ghanshyam Bhatt
Department of Mathematical Sciences
Tennessee State University
Nashville, TN 37209, USA
email: gbhatt@tnstate.edu
|
|---|
 |
Ishwari J. Kunwar
Department of Mathematics and Computer Science
Fort Valley State University
Fort Valley, GA 31030, USA
email: kunwari@fvsu.edu
|
|---|
 |
Rajan Puri
Department of Mathematics
Wake Forest University
Winston-Salem, NC 27109, USA
email: purir@wfu.edu
|
|---|
 |
Min Ranabhat
Department of Mathematical Sciences
University of Delaware
EWG 315, Newark, DE 19716, USA
email: ranabhat@udel.edu
|
|---|
Return to the EJDE web page
 be a real reflexive Banach space and
be a real reflexive Banach space and
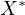 be its dual space.
Let
be its dual space.
Let
 and
and
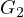 be open subsets of
be open subsets of
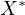 such that
such that
 ,
,
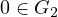 , and
, and
 is bounded.
Let
is bounded.
Let
 be a densely defined linear maximal
monotone operator,
be a densely defined linear maximal
monotone operator,
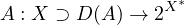 be a maximal monotone and positively
homogeneous operator of degree
be a maximal monotone and positively
homogeneous operator of degree
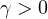 ,
,
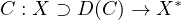 be a bounded
demicontinuous operator of type
be a bounded
demicontinuous operator of type
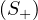 with respect to
with respect to
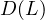 , and
, and
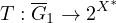 be a compact and upper-semicontinuous operator whose values
are closed and convex sets in
be a compact and upper-semicontinuous operator whose values
are closed and convex sets in
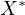 .
We first take
.
We first take
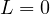 and establish the existence of nonzero solutions of
and establish the existence of nonzero solutions of
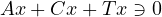 in the set
in the set
 .
Secondly, we assume that
.
Secondly, we assume that
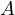 is bounded and establish the existence of nonzero solutions
of
is bounded and establish the existence of nonzero solutions
of
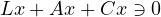 in
in
 .
We remove the restrictions
.
We remove the restrictions
![$\gamma\in (0, 1]$](images/a19x.png) for
for
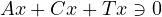 and
and
 for
for
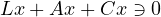 from such existing results in the literature.
We also present applications to elliptic and parabolic partial differential equations
in general divergence form satisfying Dirichlet boundary conditions.
from such existing results in the literature.
We also present applications to elliptic and parabolic partial differential equations
in general divergence form satisfying Dirichlet boundary conditions.





