Electron. J. Differential Equations, Vol. 2022 (2022), No. 75, pp. 1-13.
Positive solutions for Kirchhoff-Schrodinger equations via Pohozaev manifold
Xian Hu, Yong-Yi Lan
Abstract:
In this article we consider the Kirchhoff-Schrodinger equation
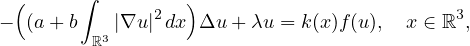
where
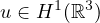 ,
,
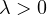 ,
,
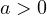 ,
,
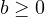 are real constants,
are real constants,
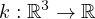 and
and
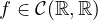 .
To overcome the difficulties that k is non-symmetric and the non-linear, and
that f is non-homogeneous, we prove the existence a positive
solution using projections on a general Pohozaev type manifold, and the
linking theorem.
.
To overcome the difficulties that k is non-symmetric and the non-linear, and
that f is non-homogeneous, we prove the existence a positive
solution using projections on a general Pohozaev type manifold, and the
linking theorem.
Submitted March 21, 2022. Published November 17, 2022.
Math Subject Classifications: 35J35, 35B38, 35J92.
Key Words: Kirchhoff-Schrodinger equation; Pohozaev manifold; Cerami sequence;
linking theorem.
DOI: https://doi.org/10.58997/ejde.2022.75
Show me the PDF file (345 KB),
TEX file for this article.
 |
Xian Hu
School of Sciences
Jimei University
Xiamen 361021, China
email: huxian19972021@163.com
|
|---|
 |
Yong-Yi Lan
School of Sciences
Jimei University
Xiamen 361021, China
email: lanyongyi@jmu.edu.cn
|
|---|
Return to the EJDE web page
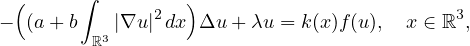
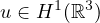 ,
,
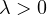 ,
,
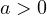 ,
,
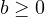 are real constants,
are real constants,
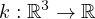 and
and
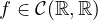 .
To overcome the difficulties that k is non-symmetric and the non-linear, and
that f is non-homogeneous, we prove the existence a positive
solution using projections on a general Pohozaev type manifold, and the
linking theorem.
.
To overcome the difficulties that k is non-symmetric and the non-linear, and
that f is non-homogeneous, we prove the existence a positive
solution using projections on a general Pohozaev type manifold, and the
linking theorem.

