Paolo Baroni, Alessandra Coscia
Abstract:
We prove C1 regularity for local vectorial minimizers of the non-autonomous functional
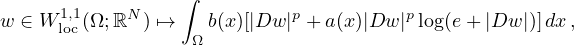
with Ω open subset of Rn, n≥2 , p>1,
0≤a(.)≤ ||a||L∞(Ω)<∞, and
0<ν≤b(.)≤ L. The result is valid provided that the function a(.)
is log-Dini continuous and that the coefficient b(.) is Dini continuous or
it is weakly differentiable and its gradient locally belongs to the Lorentz space
Ln,1(Ω;Rn).
Submitted November 1, 2022. Published November 23, 2022.
Math Subject Classifications: 35J15, 35J60, 35J99.
Key Words: Non-autonomous functionals; gradient continuity; Dini continuous coefficients.
DOI: https://doi.org/10.58997/ejde.2022.80
Show me the PDF file (486 KB), TEX file for this article.
 |
Paolo Baroni Department of Mathematical Physical and Computer Sciences University of Parma I-43124 Parma, Italy email: paolo.baroni@unipr.it |
|---|---|
 |
Alessandra Coscia Department of Mathematical Physical and Computer Sciences University of Parma I-43124 Parma, Italy email: alessandra.coscia@unipr.it |
Return to the EJDE web page