Fourth Mississippi State Conference on
Differential Equations and Computational Simulations,
Electron. J. Diff. Eqns., Conf. 03, 1999, pp. 63-73.
Uniqueness implies existence for discrete fourth order Lidstone
boundary-value problems
Johnny Henderson & Alvina M. Johnson
Abstract:
We study the fourth order difference equation

where
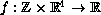 is continuous and the equation
is continuous and the equation
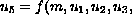
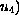 can be
solved for
can be
solved for
 as a continuous function of
as a continuous function of
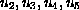 for each
for each
 .
It is shown that the uniqueness of solutions implies
the existence of solutions for Lidstone boundary-value problems on
.
It is shown that the uniqueness of solutions implies
the existence of solutions for Lidstone boundary-value problems on
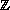 .
To this end we use shooting and topological methods.
.
To this end we use shooting and topological methods.
Published July 10, 2000.
Math Subject Classifications: 39A10, 34B10, 34B15.
Key Words: Difference equation, uniqueness, existence.
Show me the
PDF file (136K),
TEX file, and other files for this article.
 |
Johnny Henderson
Department of Mathematics,
Auburn University
Auburn, AL 36849, USA
email: hendej2@mail.auburn.edu |
tr> | Alvina M. Johnson
Department of Mathematics,
Auburn University
Auburn, AL 36849, USA
e-mail: johnso25@mail.fvsu.edu |
Return to the EJDE web page

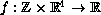 is continuous and the equation
is continuous and the equation
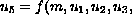
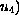 can be
solved for
can be
solved for
 as a continuous function of
as a continuous function of
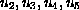 for each
for each
 .
It is shown that the uniqueness of solutions implies
the existence of solutions for Lidstone boundary-value problems on
.
It is shown that the uniqueness of solutions implies
the existence of solutions for Lidstone boundary-value problems on
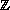 .
To this end we use shooting and topological methods.
.
To this end we use shooting and topological methods.