16th Conference on Applied Mathematics, Univ. of Central Oklahoma,
Electron. J. Diff. Eqns., Conf. 07, 2001, pp. 47-59.

A new a priori estimate for multi-point boundary-value problem

Chaitan P. Gupta

Abstract:
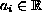Let $f:[0,1]\times \mathbb{R}^2\to \mathbb{R}$ be a function satisfying Caratheodory's conditions and $e(t)\in L^{1}[0,1]$. Let and $a_i\in \mathbb{R}$ for $i=1,2,\dots ,m-2$ be given. A priori estimates of the form
$$ \|x\|_{\infty }\leq C\| x''\|_1, \quad \|x'\|_{\infty }\leq C\|x''\|_1, $$
are needed to obtain the existence of a solution for the multi-point boundary-value problem

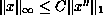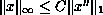using Leray Schauder continuation theorem. The purpose of this paper is to obtain a new a priori estimate of the form $\| x\|_{\infty }\leq C\| x''\|_1$. This new estimate then enables us to obtain a new existence theorem. Further, we obtain a new a priori estimate of the form $\| x\|_{\infty }\leq C\| x''\|_1$ for the three-point boundary-value problem

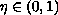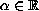where $\eta \in (0,1)$ and $\alpha \in \mathbb{R}$ are given. The estimate obtained for the three-point boundary-value problem turns out to be sharper than the one obtained by particularizing the $m$-point boundary value estimate to the three-point case.

Published July 20, 2001.
Subject lassfications: 34B10, 34B15, 34G20.
Key words: Three-point boundary-value problem, $m$-point boundary-value problem, a-priori estimates, Leray-Schauder Continuation theorem, Caratheodory's conditions.

Show me the PDF file (265K), TEX file, and other files for this article.

Chaitan P. Gupta
Department of Mathematics
University of Nevada, Reno
Reno, NV 89557 USA
email: gupta@unr.edu   chaitang@hotmail.com

Return to the EJDE web page