2002-Fez conference on Partial Differental Equations,
Electron. J. Diff. Eqns., Conf. 09, 2002, pp. 77-92.
A polyharmonic analogue of a Lelong theorem and
polyhedric harmonicity cells
Mohamed Boutaleb
Abstract:
We prove a polyharmonic analogue of a Lelong theorem using
the topological method presented by Siciak for harmonic functions.
Then we establish the harmonicity cells of a union, intersection,
and limit of domains of
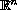 .
We also determine
explicitly all the extremal points and support hyperplanes of
polyhedric harmonicity cells in
.
We also determine
explicitly all the extremal points and support hyperplanes of
polyhedric harmonicity cells in
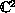 .
.
Published December 28, 2002.
Subject classfications: 31A30, 31B30, 35J30.
Key words: Harmonicity cells, polyharmonic functions, extremal points,
Lelong transformation.
Show me the
PDF file (266K),
TEX file for this article.
 |
Mohamed Boutaleb
Departement de Mathematiques et Informatique
Faculte des Sciences Dhar-Mahraz
B. P. 1796 Atlas, Fes, Maroc
e-mail: mboutalebmoh@yahoo.fr |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
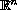 .
We also determine
explicitly all the extremal points and support hyperplanes of
polyhedric harmonicity cells in
.
We also determine
explicitly all the extremal points and support hyperplanes of
polyhedric harmonicity cells in
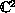 .
.
