2002-Fez conference on Partial Differental Equations,
Electron. J. Diff. Eqns., Conf. 09, 2002, pp. 139-147.
Nonlinear elliptic systems with exponential nonlinearities
Said El Manouni & Abdelfattah Touzani
Abstract:
In this paper we investigate the existence of solutions for
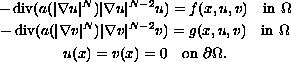
Where
 is a bounded domain in
is a bounded domain in
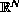 ,
,
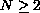 ,
,
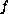 and
and
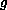 are nonlinearities having an exponential growth on
are nonlinearities having an exponential growth on
 and
and
 is a continuous function satisfying some
conditions which ensure the existence of solutions.
is a continuous function satisfying some
conditions which ensure the existence of solutions.
Published December 28, 2002.
Subject classfications: 35J70, 35B45, 35B65.
Key words: Nonlinear elliptic system, exponential growth,
Palais-Smale condition.
Show me the
PDF file (201K),
TEX file for this article.
 |
Said El Manouni
Department of Mathematics and Informatic,
Faculty of Sciences Dhar-Mahraz,
P.O. Box 1796 Atlas-Fez, Morocco
e-mail: manouni@hotmail.com |
 |
Abdelfattah Touzani
Department of Mathematics and Informatic,
Faculty of Sciences Dhar-Mahraz,
P.O. Box 1796 Atlas-Fez, Morocco
e-mail: atouzani@iam.net.ma |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
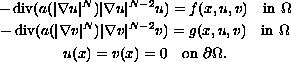
 is a bounded domain in
is a bounded domain in
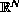 ,
,
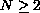 ,
,
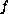 and
and
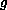 are nonlinearities having an exponential growth on
are nonlinearities having an exponential growth on
 and
and
 is a continuous function satisfying some
conditions which ensure the existence of solutions.
is a continuous function satisfying some
conditions which ensure the existence of solutions.

