2002-Fez conference on Partial Differental Equations,
Electron. J. Diff. Eqns., Conf. 09, 2002, pp. 183-202.
Nonlinear equations with natural growth terms and measure data
Alessio Porretta
Abstract:
We consider a class of nonlinear elliptic equations containing
a
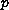 -Laplacian
type operator, lower order terms having natural
growth with respect to the gradient, and bounded measures as data.
The model example is the equation
-Laplacian
type operator, lower order terms having natural
growth with respect to the gradient, and bounded measures as data.
The model example is the equation
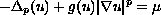
in a bounded set
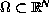 , coupled with a
Dirichlet boundary condition. We provide a review of the
results recently obtained in the absorption case (when
, coupled with a
Dirichlet boundary condition. We provide a review of the
results recently obtained in the absorption case (when
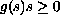 )
and prove a new existence result without any sign condition on
)
and prove a new existence result without any sign condition on
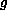 ,
assuming only that
,
assuming only that
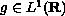 .
This latter assumption is
proved to be optimal for existence of solutions for any measure
.
This latter assumption is
proved to be optimal for existence of solutions for any measure
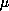 .
.
Published December 28, 2002.
Subject classfications: 35J60, 35J65, 35R05.
Key words: Nonlinear elliptic equations, natural growth terms, measure data.
Show me the
PDF file (255K),
TEX file for this article.
 |
Alessio Porretta
Dipartimento di Matematica,
Universita di Roma "Tor Vergata",
Via della Ricerca Scientifica 1,
00133, Roma, Italia.
email: porretta@mat.uniroma2.it |
Return to the table of contents
for this conference.
Return to the Electronic Journal of Differential Equations
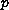 -Laplacian
type operator, lower order terms having natural
growth with respect to the gradient, and bounded measures as data.
The model example is the equation
-Laplacian
type operator, lower order terms having natural
growth with respect to the gradient, and bounded measures as data.
The model example is the equation
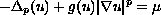
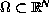 , coupled with a
Dirichlet boundary condition. We provide a review of the
results recently obtained in the absorption case (when
, coupled with a
Dirichlet boundary condition. We provide a review of the
results recently obtained in the absorption case (when
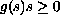 )
and prove a new existence result without any sign condition on
)
and prove a new existence result without any sign condition on
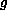 ,
assuming only that
,
assuming only that
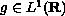 .
This latter assumption is
proved to be optimal for existence of solutions for any measure
.
This latter assumption is
proved to be optimal for existence of solutions for any measure
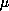 .
.
