Fifth Mississippi State Conference on Differential Equations and Computational Simulations,
Electron. J. Diff. Eqns., Conf. 10, 2003, pp. 143-152.

A non-resonant multi-point boundary-value problem for a p-Laplacian type operator

Chaitan P. Gupta

Abstract:
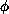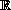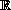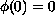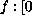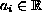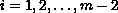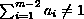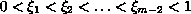Let $\phi $ be an odd increasing homeomorphism from $\mathbb{R}$ onto $\mathbb{R}$ with $\phi (0)=0$, $f:[0$, $1]\times \mathbb{R}^{2}\to \mathbb{R}$ be a function satisfying Caratheodory's conditions and $e(t)\in L^{1}[0,1]$. Let $\xi_{i}\in (0,1)$, $a_{i}\in \mathbb{R}$, $i=1,2, \dots , m-2$, $\sum_{i=1}^{m-2}a_{i}\neq 1$, $0 lessthan \xi_{1} less than \xi_{2}less than \dots less than \xi_{m-2} less than 1$ be given. This paper is concerned with the problem of existence of a solution for the multi-point boundary-value problem
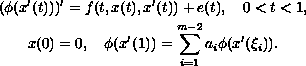
$$\displaylines{ (\phi (x'(t)))'=f(t,x(t),x'(t))+e(t),\quad 0 less than t less than 1, \cr x(0)=0, \quad \phi (x'(1))=\sum_{i=1}^{m-2}a_{i}\phi(x'(\xi_{i})). }$$
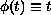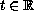This paper gives conditions for the existence of a solution for the above boundary-value problem using some new Poincare type a priori estimates. In the case $\phi (t)\equiv t$ for $t\in \mathbb{R}$, this problem was studied earlier by Gupta, Trofimchuk in [2] and by Gupta, Ntouyas and Tsamatos in [1]. We give a priori estimates needed for this problem that are similar to a priori estimates obtained by Gupta, Trofimchuk in [2]. We then obtain existence theorems for the above multi-point boundary-value problem using the a priori estimates and Leray-Schauder continuation theorem.

Published February 28, 2003.
Subject classifications: 34B10, 34B15, 34G20.
Key words: Multi-point boundary-value problem, three-point boundary-value problem, p-Laplacian, Leray Schauder Continuation theorem, Caratheodory's conditions.

Show me the PDF file (210K), TEX file, and other files for this article.

Chaitan P. Gupta
Department of Mathematics, 084
University of Nevada, Reno
Reno, NV 89557, USA
email: gupta@unr.edu

Return to the table of contents for this conference.
Return to the Electronic Journal of Differential Equations