Thermal equilibrium states of superconductors are governed by the nonlinear problem
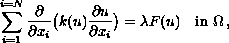
with boundary condition
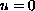 . Here the domain
. Here the domain
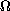 is an open
subset of
is an open
subset of
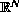 with smooth boundary.
The field
with smooth boundary.
The field
 represents the thermal state, which we assume is in
represents the thermal state, which we assume is in
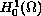 . The state
. The state
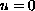 models the superconductor's
state which is the unique physically meaningful solution.
In previous works, the superconductor domain is unidirectional
while in this paper we consider a domain with arbitrary
geometry. We obtain the following results:
A set of criteria that leads to uniqueness of a superconductor state,
a study of the existence of normal states and the number of them,
and optimal criteria when the geometric dimension is 1.
models the superconductor's
state which is the unique physically meaningful solution.
In previous works, the superconductor domain is unidirectional
while in this paper we consider a domain with arbitrary
geometry. We obtain the following results:
A set of criteria that leads to uniqueness of a superconductor state,
a study of the existence of normal states and the number of them,
and optimal criteria when the geometric dimension is 1. 