2004-Fez conference on Differential Equations and Mechanics.
Electron. J. Diff. Eqns.,
Conference 11, 2004, pp. 167-173.
Stability and Hopf bifurcation in
a haematopoietic stem cells model
Hamad Talibi Alaoui, Radouane Yafia
Abstract:
We consider the Haematopoietic Stem Cells (HSC) Model
with one delay, studied by Mackey [4,5]
and Andersen and Mackey [1].
There are two possible stationary states in the model. One of them
is trivial, the second
 ,
depending on the delay,
may be non-trivial . This paper investigates the stability of
the non trivial state as well as the occurrence of the Hopf
bifurcation depending on time delay.
We prove the existence and uniqueness of a critical values
,
depending on the delay,
may be non-trivial . This paper investigates the stability of
the non trivial state as well as the occurrence of the Hopf
bifurcation depending on time delay.
We prove the existence and uniqueness of a critical values
 and
and
 of the delay such that
of the delay such that
 is asymptotically stable for
is asymptotically stable for
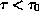 and unstable for
and unstable for
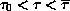 .
We show that
.
We show that
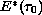 is a Hopf bifurcation critical
point for an approachable model.
is a Hopf bifurcation critical
point for an approachable model.
Published October 15, 2004
Math Subject Classifications: 34K18
Key Words: Haematopoietic stem cells model; delayed differential equations;
Hopf bifurcation; periodic solutions.
Show me the
PDF file (203K),
TEX file for this article.
 |
Hamad Talibi Alaoui
Université Chouaib Doukkali Faculté des Sciences
Département de Mathématiques et Informatique
B.P. 20, El Jadida, Morocco
email: talibi@math.net |
|---|
 |
Radouane Yafia
Université Chouaib Doukkali Faculté des Sciences
Département de Mathématiques et Informatique
B. P. 20, El Jadida, Morocco
email: yafia_radouane@hotmail.com |
|---|
Return to the EJDE web page
 ,
depending on the delay,
may be non-trivial . This paper investigates the stability of
the non trivial state as well as the occurrence of the Hopf
bifurcation depending on time delay.
We prove the existence and uniqueness of a critical values
,
depending on the delay,
may be non-trivial . This paper investigates the stability of
the non trivial state as well as the occurrence of the Hopf
bifurcation depending on time delay.
We prove the existence and uniqueness of a critical values
 and
and
 of the delay such that
of the delay such that
 is asymptotically stable for
is asymptotically stable for
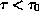 and unstable for
and unstable for
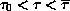 .
We show that
.
We show that
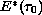 is a Hopf bifurcation critical
point for an approachable model.
is a Hopf bifurcation critical
point for an approachable model.
